Операція об’єднання (додавання) множин та основні властивості (закони) цієї операції.

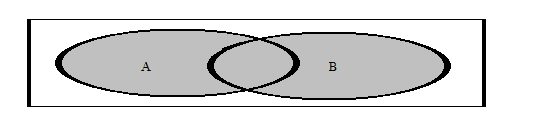
4. Розглянемо дві множини: А={2,3,4} і В={2,4,6}. Утворимо нову множину С={2,3,4,6}. Із яких елементів складається множина С? – із елементів, які входять хоча б в одну із множин. Множину С, яка складається із елементів, що належать хоча б одній із множин А чи В, називають об’єднанням множин А і В. Її позначають С=АÈB.

Означення: Об’єднанням множин А та В називають третю множину АÈВ, що складається із елементів, які входять хоча б в одну із множин А чи В.

Символічно наведене означення можна записати так: АÈВ={х /хÎА або аÎВ}. На діаграмі Ейлера-Венна ця множина зображена на малюнку № 1.6.

Малюнок № 1.6. об’єднання множин АÈВ.

Операція об’єднання може поширюватись на три і більше множин. Вона підкоряється певним законам, серед яких є такі, справедливість яких випливає безпосередньо із означення об’єднання, та такі, які слід доводити. До законів (властивостей) об’єднання, справедливість яких легко обґрунтувати, виходячи із означення об’єднання множин, відносяться: 1. AÈÆ=A. 2. AÈU=U. 3. AÈA=A - закон ідемпотентності (незмінності).

До законів, які слід доводити одним із можливих способів (міркуваннями або за допомогою діаграм Ейлера-Венна) відноситься переставний або комутативний закон: AÈB=BÈA. Для його доведення використовуємо діаграми Ейлера-Венна. Намалюємо дві однакові діаграми, на лівій із яких зображатимемо ліву частину рівності, а на правій – праву. На лівій діаграмі заштрихуємо множину A горизонтальними штрихами, а множину B - вертикальними. Множина AÈB зображається тією частиною універсальної множини, де є або горизонтальні, або вертикальні штрихи. На правій діаграмі множину A заштрихуємо вертикальними штрихами, а множину В - горизонтальними. Множина BÈA зображається на правій діаграмі тією частиною універсальної множини, де є або вертикальні, або горизонтальні штрихи. Порівнюючи їх, бачимо, що множини AÈB і BÈA зображаються на них однаковими частинами універсальної множини, а тому можна стверджувати, що AÈB=BÈA. Закон доведено (див. малюнок № 1.7.).

АÈВ ВÈА

Малюнок № 1.7. Доведення переставного закону AÈB=BÈA.

Доведемо сполучний або асоціативний закон (AÈB)ÈС=AÈ(BÈС) за допомогою міркувань. Оскільки дві множини вважаються рівними, якщо кожен елемент першої множини є елементом другої і, навпаки, кожен елемент другої множини є елементом першої множини, то доведення складається з двох частин. У першій частині доведемо, що кожен елемент, що належить лівій частині асоціативного закону, є елементом і правої частини.

1. Нехай хÎ(AÈB)ÈС. Згідно означення об’єднання множин це означає, що: або 1) хÎ(AÈB), або 2) хÎС, або 3) хÎAÈB і хÎС. Якщо хÎAÈB, то або 1) хÎA, або 2) хÎB, або 3) хÎA і хÎB. Якщо хÎA, то, переходячи до правої частини закону, на основі означення об’єднання множин можна стверджувати, що хÎAÈ(BÈС). Якщо хÎB, то хÎBÈС, тобто хÎAÈ(BÈС). Якщо хÎA і хÎB, то хÎAÈ(BÈС). Якщо ж, нарешті, хÎС, то хÎ(BÈС), а тому хÎAÈ(BÈС). Таким чином ми показали, що будь-який елемент лівої частини рівності належить правій частині рівності. Оскільки елемент у лівій частині ми вибирали довільно, то наші міркування можна повторити для будь-якого елемента лівої частини. Отже, кожен елемент лівої частини рівності є елементом правої частини рівності. Перша частина теореми доведена.

2. Доведемо, що кожен елемент правої частини є елементом лівої. Нехай уÎAÈ(BÈС). Згідно означення об’єднання множин можливі такі випадки: або 1) уÎA, або 2) уÎBÈС, або 3) уÎA і уÎBÈС. Якщо уÎA, то уÎAÈB, а тому уÎ(AÈB)ÈС. Якщо уÎBÈС, то або 1) уÎB, або б) уÎС, або в) уÎB і уÎС. Якщо уÎB, то уÎAÈB тоді уÎ(AÈB)ÈС. Якщо уÎС, то уÎ(AÈB)ÈС. Якщо уÎB і уÎС, то уÎ(AÈB)ÈС. Аналогічно легко довести справедливість рівності у випадку, коли уÎA і уÎBÈС. Оскільки елемент у в правій частині ми вибрали довільно, то наші міркування можна повторити для кожного із елементів правої частини. Отже, кожен елемент правої частини є елементом лівої. Другу частину теореми доведено.

Таким чином, кожен елемент лівої частини є елементом правої частини і, навпаки. А тому, ліва і права частини рівності складаються з одних і тих самих елементів. А це означає, що (AÈB)ÈС=AÈ(BÈС). Закон доведено.

Приклад: утворити об’єднання множин А та В, якщо множина А={1,2,3,4,5}, а В={а,в,с}. AÈB={1,2,3,4,5,а,в,с}.

Поиск по сайту: