 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Экономико-математическое моделирование как способ изучения хозяйственной деятельности
Математическое моделирование экономических явлений и процессов – важный инструмент экономического анализа. Дает возможность получить четкое представление об исследуемом объекте, охарактеризовать и количественно описать его внутреннюю структуру и внешние связи. Модель - условный образ объекта управления (исследования). Модель отображает характеристики объекта: свойства, взаимосвязи, структурные и функциональные параметры, существенные для цели управления (исследования). Главным образом используются математические модели, изучаемое явление или процесс с помощью уравнений, неравенств, функций и других математических средств: - С количественными характеристиками, записанными в виде формул; - Числовые с конкретными числовыми характеристиками; - Логические, записанные с помощью логических выражений; - Графические, выраженные в графических образах. Этапы процесса моделирования: 1. Анализ теоретических закономерностей, свойственных изучаемому явлению или процессу, и эмпирических данных о его структуре и особенностях; 2. Определение методов, с помощью которых можно решить задачу; 3. Анализ полученных результатов. Важный момент первого этапа – четкая формулировка конечной цели построения модели и определение критерия, по которому будут сравниваться различные варианты решения. Критерии: наибольшая прибыль, наименьшие издержки производства, максимальная загрузка оборудования, производительность труда. Критерий отражается целевой функцией. Обычно предполагается ограниченность ресурсов (система ограничений). Общая постановка задачи:
где
Вторым этапом моделирования экономических процессов является выбор наиболее рационального математического метода для решения задачи. Третьим этапом моделирования является всесторонний анализ результата, полученного при изучении экономического явления или процесса. Критерии достоверности и качества: практика, соответствие полученных результатов и выводов реальным условиям производства, экономическая содержательность полученных оценок. В детерминированном моделировании факторных систем можно выделить небольшое число наиболее часто встречающихся типов конечных факторных систем: Аддитивные модели Мультипликативные модели Кратные модели
- - - - - - Основные приемы моделирования: 1. Метод удлинения факторной системы. Исходная модель 2. Метод расширения факторной системы. Исходная модель 3. Метод сокращения факторной системы. Исходная модель Таким образом, сложный процесс формирования уровня изучаемого показателя хозяйственной деятельности может быть разложен различными приемами на его составляющие и представлен в виде модели детерминированной факторной системы. Так же большое распространение получили стохастические модели, которые основаны на эмпирических данных. Необходим только количественный анализ эмпирических данных: оценка связи и корреляции между показателями, оценка статистической значимости связей, регрессионный анализ, группировка многомерных наблюдений, компонентный анализ.
Поиск по сайту: |
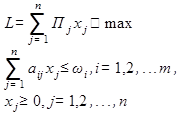
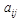 - норма расхода i-того производственного ресурса на производство единицы j-того продукта;
- норма расхода i-того производственного ресурса на производство единицы j-того продукта; - запасы i-того вида производственного ресурса на рассматриваемый период времени;
- запасы i-того вида производственного ресурса на рассматриваемый период времени; - количество производимой продукции j-того вида;
- количество производимой продукции j-того вида; - прибыль, получаемая от производства единицы продукции j-того вида.
- прибыль, получаемая от производства единицы продукции j-того вида.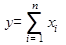


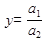 . Если представить
. Если представить  в виде суммы отдельных слагаемых-факторов
в виде суммы отдельных слагаемых-факторов  , то
, то  - конечная факторная система.
- конечная факторная система. , т.е. мультипликативную модель вида
, т.е. мультипликативную модель вида  .
. . В данном случае имеем конечную факторную систему вида
. В данном случае имеем конечную факторную систему вида  .
.