 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теорема о переходе к пределу в показателе степени при постоянном основании ⇐ ПредыдущаяСтр 9 из 9
В показателе степени при постоянном основании можно переходить к пределу, то есть Умения 1. Раскрыть неопределенности вида: Решение.
2. Раскрыть неопределенности вида: Решение.
3. Раскрыть неопределенности вида: Решение.
4. Раскрыть неопределенности вида: Решение.
5. Вычислить предел дроби, содержащей иррациональность. Решение.
6. Вычислить пределы выражений, содержащих логарифмы, показательные, степенные, показательно-степенные и тригонометрические функций. · Выражение, содержащее логарифмы:
· Выражение, содержащее тригонометрические функции:
· Выражение, содержащее степенную функцию:
· Выражение, содержащее показательную функцию:
Решение: Решим с помощью логарифмирования:
Найдем производную:
Рассмотрим предел при
· Выражение, содержащее показательно-степенную функцию:
26. Нахождение предела кусочно-заданной функции
Умения 1.Найти предел кусочно-заданной функции. Дана функция Найти предел при Решение. Так как нам нужно найти предел при
Ответ: предел функции при 27. Нахождение односторонних пределов Понятия 8.Число 9.Число
Умения 1. Найти односторонние пределы функции Решение. Рассмотрим предел справа:
Рассмотрим предел слева:
2. Найти односторонние пределы функции Решение. Рассмотрим предел слева:
Рассмотрим предел справа:
28. Нахождение односторонних пределов у функций с параметром
Понятия 8.Число 9.Число
Умения 1.Нахождение односторонних пределов у функции с параметром. Дан предел функции с параметром Найти данный предел. Решение.
Предположим, что
29. Нахождение пределов функции одной переменной при n, стремящемся к бесконечности
Умения 1. Нахождение пределов функции одной переменной при Найти Решение:
Умножив и разделив выражение, находящееся под знаком предела, на
30. Частичный предел функции. Нахождение нижнего и верхнего пределов функций Понятия 24.Число
25. Нижним пределом функции 26. Верхним пределом функции Умения 1.Найти нижний и верхний предел функции. Дана функция Решение. Рассмотрим предел данной функции при
Он принимает такое значение при 0 и Ответ. 0 – нижний предел,
Поиск по сайту: |
 , где
, где  ,
,  или
или  ,
,  .
.


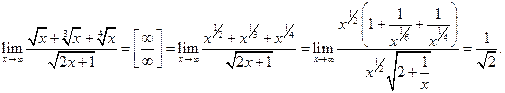


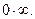




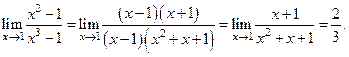


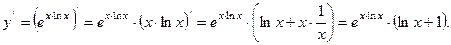
 от полученной производной:
от полученной производной:

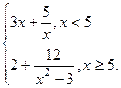
 .
. 

 называется правым пределом функции
называется правым пределом функции  в точке
в точке  (
( 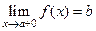 ), если для любого положительного числа
), если для любого положительного числа  найдется отвечающее ему положительное число
найдется отвечающее ему положительное число  такое, что для всех значений аргумента
такое, что для всех значений аргумента  , удовлетворяющих условию
, удовлетворяющих условию 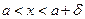 справедливо неравенство
справедливо неравенство  .
. ), если для любого положительного числа
), если для любого положительного числа  справедливо неравенство
справедливо неравенство 





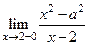 .
. .
.
 .
. .
. ,если
,если .
. , получим
, получим
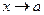 ), если существует последовательность значений аргумента
), если существует последовательность значений аргумента  , сходящаяся к
, сходящаяся к  , отличных от
, отличных от  сходится к числу
сходится к числу 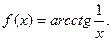 Найти нижний и верхний пределы функции при
Найти нижний и верхний пределы функции при  .
.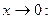

 . Получаем, что 0 и
. Получаем, что 0 и