 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Геометрический смысл предела функции на бесконечности
Если
Умения 1. Найти предел функции на бесконечности.
2. Найти предел функции на бесконечности.
4. Связь между предельным значением и значением функции в точке, междуодносторонними пределами и пределом Понятия 8.Число 9.Число
Утверждения Связь между предельным значением и значением функции в точке Предельное значение функции 1. Существует левое предельное значение. 2. Существует правое предельное значение. 3. Левое и правое предельные значения совпадают. 14. Предел элементарной функции при x, стремящемся к значению, которое входит в область ее определения Если в точке 5. Колебания функции f на множестве E из D(f)
Понятия 27. Колебанием функции f на множестве
Умения 1.Нахождение колебания функции. Дана функция Решение. Рассмотрим пределы функции на конечных точках первого интервала:
Колебание функции будет равно:
Рассмотрим пределы функции на конечных точках второго интервала:
Колебание функции будет равно:
II. Бесконечно малые и бесконечно большие функции
6. Понятие бесконечно малой и бесконечно большой функции
Понятия 10.Функция 11.Функция 16. Простейшей бесконечно малой называется величина вида Утверждения
Поиск по сайту: |
 , то выполняется условие такое, что
, то выполняется условие такое, что 
 .
.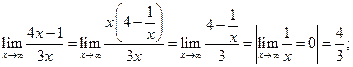

 называетсяправым пределом функции
называетсяправым пределом функции  в точке a(
в точке a( 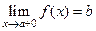 ), если для любого положительного числа
), если для любого положительного числа  найдется отвечающее ему положительное число
найдется отвечающее ему положительное число  такое, что для всех значений аргумента
такое, что для всех значений аргумента  , удовлетворяющих условию
, удовлетворяющих условию 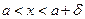 справедливо неравенство
справедливо неравенство  ), если для любого положительного числа
), если для любого положительного числа  справедливо неравенство
справедливо неравенство  в точке
в точке  существует тогда, когда выполняются следующие условия:
существует тогда, когда выполняются следующие условия: существуют конечные и равные между собой левое и правое предельные значения, то в точке
существуют конечные и равные между собой левое и правое предельные значения, то в точке 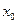 существует предельное значение этой функции, равное значению односторонних пределов.
существует предельное значение этой функции, равное значению односторонних пределов.  .
. из
из  называется наибольшая разность между наибольшем и наименьшем значениями на
называется наибольшая разность между наибольшем и наименьшем значениями на  , где
, где 
 . Найти колебание данной функции на интервалах
. Найти колебание данной функции на интервалах  и
и  .
.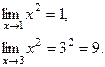


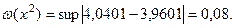
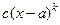 , где
, где 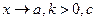 - постоянный коэффициент.
- постоянный коэффициент.