|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теорема о замене бесконечной малых функций им эквивалентным
При раскрытии неопределенностей вида
Умения 1.Сравнивать бесконечно малые функции. Решение: Это бесконечно малые функции.
функции эквивалентны -
Решение: Это бесконечно малые функции.
Так как предел равен конечному числу, отличному от нуля, то функции
Решение: Это бесконечно малые функции.
функция
Решение: Это бесконечно большие функции.
13. Нахождение порядка малости бесконечно малой функции Понятия 10.Функция 18.Простейшая бесконечно малая
Умения 1.Найти порядок малости бесконечно малой функции.
Решение. Данная функция является бесконечно малой, поэтому для того чтобы найти ее порядок малости, необходимо сравнить ее с бесконечно малой функцией. Для этого возьмем простейшую бесконечно малую функцию
2.Найти порядок малости бесконечно малой функции Решение. Данная функция является бесконечно малой, поэтому для того чтобы найти ее порядок малости, необходимо сравнить ее с бесконечно малой функцией. Для этого возьмем простейшую бесконечно малую функцию
14. Нахождение порядка роста бесконечно большой функции Понятия 11.Функция 19.Пусть 20.Пусть 21.Пусть 22.Пусть 23.Простейшая бесконечно большая Умения 1. Найти порядок роста бесконечно большой функции Решение. Данная функция является бесконечно большой, поэтому для того чтобы найти ее порядок роста, необходимо сравнить ее с бесконечно большой функцией. Для этого возьмем простейшую бесконечно большую функцию
2.Найти порядок роста бесконечно большой функции Решение. Данная функция является бесконечно большой, поэтому для того чтобы найти ее порядок роста, необходимо сравнить ее с бесконечно большой функцией. Для этого возьмем простейшую бесконечно большую функцию
15. Нахождение главной части бесконечно малой и бесконечно большой функции Понятия 17.Простейшая бесконечно малая 23.Простейшая бесконечно большая
Умения 1. Выделить главную часть бесконечно малой функции и бесконечно большой функции. Решение. Это бесконечно малая функция. Поэтому сравниваем с простейшей бесконечно малой функцией.
2. Выделить главную часть бесконечно малой функции и бесконечно большой функции. Решение. Это бесконечно большая функция. Поэтому сравниваем с простейшей бесконечно большой функцией.
16. Погрешность, совершаемая при замене бесконечно малой функции ее главнойчастью Утверждения
Поиск по сайту: |
 , при вычислении пределов сомножители можно заменять эквивалентными бесконечно малыми.
, при вычислении пределов сомножители можно заменять эквивалентными бесконечно малыми.




 и
и 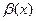 одного порядка малости.
одного порядка малости.

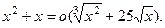
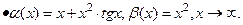
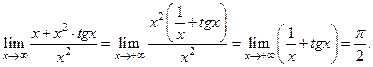
 и
и  одного порядка роста.
одного порядка роста. называется бесконечно малой в точке
называется бесконечно малой в точке  , если предел этой функции в точке
, если предел этой функции в точке 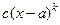 , где
, где 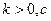 - постоянный коэффициент, эквивалентная бесконечно малой
- постоянный коэффициент, эквивалентная бесконечно малой  (
(  ), называется ее главной частью, а
), называется ее главной частью, а  - порядком малости.
- порядком малости.
 при
при  . И рассмотрим в пределе их отношение.
. И рассмотрим в пределе их отношение.
 порядок малости.
порядок малости. .
.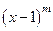 при
при  . И рассмотрим в пределе их отношение.
. И рассмотрим в пределе их отношение.
 порядок малости.
порядок малости. и
и  - две функции, заданные для одних и тех же значений аргумента и обе являющиеся бесконечно большими в точке
- две функции, заданные для одних и тех же значений аргумента и обе являющиеся бесконечно большими в точке  . Функции
. Функции  равен конечному числу, отличному от нуля.
равен конечному числу, отличному от нуля.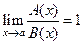 .
. , и обозначается
, и обозначается 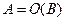 .
.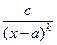 , где
, где 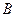 , называется ее главной частью, а
, называется ее главной частью, а 
 при
при 
 - порядок роста.
- порядок роста.
 при
при  . И рассмотрим в пределе их отношение.
. И рассмотрим в пределе их отношение.


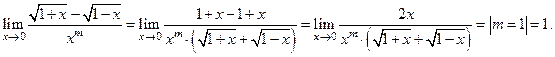
 главная часть равна
главная часть равна 


 главная часть равна
главная часть равна