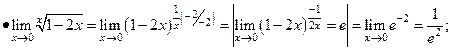 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Первый замечательной предел
Первый замечательный предел
Умения 1.Первый замечательный предел. Даны пределы: Решить при помощи первого замечательного предела. Решение.
23. Второй замечательный предел Понятия 4.Число 5.Число 6.Число 7.Число Утверждения Второй замечательной предел Второй замечательный предел
Умения 1. Раскрыть неопределенности вида: Решение.
2.Раскрыть неопределенности вида: Решение.
Воспользуемся утверждением:
Получим:
3.Раскрыть неопределенности вида: Решение. Из утверждения:
Получаем:
4. Второй замечательный предел. Даны пределы:
Решить с помощью второго замечательного предела. Решение.
24. Нахождение параметров, при которых предел функции равен данному числу
Умения 1. Нахождение параметра, при котором предел функции равен данному числу
Решение. В данном случае рассмотрим коэффициенты при старших степенях:
2. Нахождение параметра, при котором предел функции равен данному числу
Решение. Подставим 0 и решим уравнение:
25. Нахождение пределов дроби, содержащей иррациональности; выражений,содержащих логарифмы, показательные и степенные функции Утверждения
Поиск по сайту: |
.
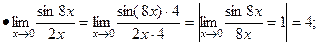
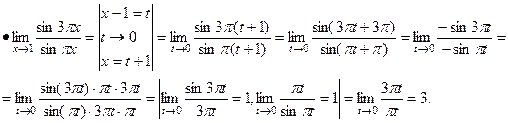
называетсяпределом (или предельным значением) функции 
(по Гейне) в точке 
(или при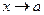 
), если для любой последовательности значений аргумента 
, сходящейся к 
, отличных от 
сходится к числу 
), если для любой бесконечно большой последовательности значений аргумента 
найдется отвечающее ему положительное число 
такое, что для всех значений аргумента 
, удовлетворяющих условию 
справедливо неравенство 
.
справедливо неравенство 
.
, при условии 
.
.
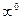
