 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Погрешность, совершаемая при замене бесконечной малой функции ее главной частью
1. При замене бесконечно малой функции 2. При замене бесконечно малой функции 3. При замене некоторой бесконечно малой величины 4. При замене некоторой бесконечно малой величины III. Теоремы о пределах функций
17. Арифметические операции над функциями, имеющими предел Понятия 4.Число 5.Число 6.Число 7.Число Утверждения Теорема о пределе алгебраической суммы двух функций Предел алгебраической суммы конечного числа функций существует и равен сумме пределов этих функций при условии, что каждая из функций имеет предел. Теорема о пределе произведения двух функций Предел произведения конечного числа функций существует и равен произведению пределов этих функций при условии, что каждая из функций имеет предел.
Поиск по сайту: |
 ее главной частью
ее главной частью 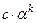 ,допускаемая при этом абсолютная погрешность
,допускаемая при этом абсолютная погрешность  будет бесконечно малой при
будет бесконечно малой при  .
. будет бесконечно малой при
будет бесконечно малой при  эквивалентной ей величиной
эквивалентной ей величиной  может быть сделана сколь угодно малой.
может быть сделана сколь угодно малой.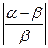 может быть сделана сколь угодно малой.
может быть сделана сколь угодно малой. называется пределом (или предельным значением) функции
называется пределом (или предельным значением) функции  (по Гейне) в точке
(по Гейне) в точке  (или при
(или при 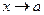 ), если для любой последовательности значений аргумента
), если для любой последовательности значений аргумента  , сходящейся к
, сходящейся к  , отличных от
, отличных от  сходится к числу
сходится к числу  ), если для любой бесконечно большой последовательности значений аргумента
), если для любой бесконечно большой последовательности значений аргумента  найдется отвечающее ему положительное число
найдется отвечающее ему положительное число  такое, что для всех значений аргумента
такое, что для всех значений аргумента  , удовлетворяющих условию
, удовлетворяющих условию  справедливо неравенство
справедливо неравенство  .
. справедливо неравенство
справедливо неравенство