 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема: Выборочное наблюдение
Выборочное наблюдение – это такое несплошное наблюдение, при котором обследованию подвергается часть единиц совокупности, а результаты распространяются на всю совокупность. Для того, чтобы выборка полно и правильно представляла генеральную совокупность, необходимо объективно произвести отбор данных. Виды, способы и методы отбора единиц для формирования выборочной совокупности представлены на схеме (рисунок 6). В случае, когда совокупность характеризуется количественным признаком, основной характеристикой выборочного наблюдения будет средний размер признака: Для характеристики альтернативного (качественного) признака исчисляют относительную величину – долю: p – по генеральной совокупности, w – по выборке. Конечная цель выборочного наблюдения – распространение полученных по выборке данных на генеральную совокупность. Это происходит с помощью предельных ошибок ∆x и ∆w :
        
Рисунок 6 - Виды, способы и методы отбора единиц в выборочную совокупность
Формулы определения предельных ошибок зависят от способа отбора единиц в выборку. Таблица 27 - Предельная ошибка выборки для различных способов отбора
Условные обозначения, принятые в формулах: t - коэффициент доверия; σ2 - дисперсия признака в выборочной совокупности;
r - число отобранных серий; R - число серий в генеральной совокупности; n - число отобранных единиц; N - число единиц в генеральной совокупности. Репрезентативность выборочных характеристик в значительной мере зависит от численности выборки. Математическая статистика разработала следующие формулы для определения необходимой численности выборки.
Таблица 28 - Необходимый объем выборки для различных способов формирования выборочной совокупности
Контрольные вопросы: 1.Понятие выборочного наблюдения. 2.Условия применения выборочного наблюдения. 3.Обобщающие характеристики генеральной и выборочной. 4.Виды отбора единиц в выборочную совокупность. 5.Способы отбора единиц в выборочную совокупность 6.Методы отбора единиц в выборочную совокупность. 7.Характеристика случайного отбора. 8. Характеристика механического отбора. 9. Характеристика типического отбора. 10.Характеристика серийного отбора. 11.Ошибки выборочного наблюдения. 12.Определение ошибок при случайном и механическом отборе. 13.Определение ошибок при типическом отборе. 14.Определение ошибок при серийном отборе. 15.Определение численности случайной и механической выборки. 16.Определение численности типической выборки. 17.Определение численности серийной выборки. 18.Понятие малой выборки, сфера ее применения.
Задание 1 При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 1240 изделий. Средний вес изделия по результатам исследования составил 3,5 кг. Значение дисперсии составило 81. Необходимо: 1) с вероятностью 0,954 определить пределы, в которых находится средний вес изделия в генеральной совокупности; 2) как изменятся пределы, в которых находится средняя по генеральной совокупности, если вероятность будет равна 0,997?
Задание 2 В цеху работает 2450 ткачей. Для определения среднего объема производства ткани в час была организована 4%-ная случайная бесповторная выборка ткачей. По ее результатам было получено следующее распределение ткачей по объему производства ткани в час:
Таблица 29 – Результаты исследования среднего выпуска продукции
С вероятностью 0,95 найдите пределы, в которых будет находиться средний объем производства ткани в генеральной совокупности.
Задание 3 С целью определения среднего удоя молока в хозяйстве с численностью доярок 146 человек в августе 2007 года была произведена 30%-ная механическая выборка. По результатам наблюдения оказалось, что у 3% исследованных фактические надои превышали 25 литров в день. С вероятностью 0,997 установите пределы, в которых находится генеральная доля доярок с удоем молока более 25 литров в день. Каковы будут результаты, если точность расчетов установить равной 0,683?
Задание 4 В партии товара, состоящей из 150 ящиков, проводилось выборочное обследование качества (доли бракованных изделий) на основе отбора серий (ящиков). Выборочные средние по ящикам составили соответственно 3%, 1,05%, 2,01%, 4,0%, 0,6%, 1,9%. С вероятностью 0,683 найдите пределы доли бракованного товара во всей партии. Задание 5 В 100 туристических агентствах города предполагается провести исследование среднего количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка не превышала 4 путевок, если по данным предварительных расчетов среднеквадратическое отклонение составляет 24?
Задание 6 Для определения доли студентов дневной формы обучения со средним баллом более 9 предполагается организовать типическую выборку пропорционально численности студентов различных курсов с механическим отбором внутри групп. Общее число студентов университета составляет 4390 человек, в. том числе: - студентов 1 курса – 1264 человека; - студентов 2 курса - 912 человек; - студентов 3 курса – 840 человек; - студентов 4 курса – 688 человек; - студентов 5 курса – 686. На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 2500. Определите необходимый объем выборки при вероятности 0,997 и ошибке 3%.
Поиск по сайту: |
 - по генеральной совокупности;
- по генеральной совокупности;  - по выборке.
- по выборке.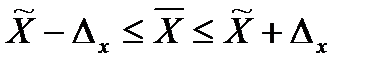 ,
, .
.












 - межсерийная дисперсия;
- межсерийная дисперсия;










