 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Кінематичні характеристики руху точки
3.2.1. Швидкість точки. Нехай рух матеріальної точки відносно вибраної системи відліку задано векторним рівнянням Величина Границя цього вектора при

В довільний момент часу формулу (3.5) можна записати у вигляді

 напрямлений вздовж січної напрямлений вздовж січної  . При зменшенні . При зменшенні  січна буде обертатися навколо точки січна буде обертатися навколо точки 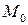 і в граничному положенні стане дотичною до траєкторії в точці і в граничному положенні стане дотичною до траєкторії в точці 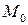 . Таким чином, вектор швидкості точки напрямлений вздовж дотичної до траєкторії в напрямку руху. . Таким чином, вектор швидкості точки напрямлений вздовж дотичної до траєкторії в напрямку руху.
Вектори Припустимо, що рух матеріальної точки задано координатним способом
Позначимо через
Величину вектора швидкості
 ; ;  ; ; 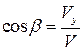 ; ; 
При натуральному способі задання руху точки рівняння руху має вигляд
На підставі формули (3.6) можна записати
Тут враховано, що

Формули (3.6)-(3.9) дозволяють визначити вектор швидкості в будь-який момент часу при довільному способі задання руху точки.
Нехай рух матеріальної точки задано векторним способом
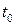 , для якого визначимо вектор , для якого визначимо вектор  . Часу . Часу 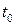 надамо приросту надамо приросту 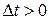 і визначимо вектор і визначимо вектор  . Вектор . Вектор 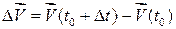 називається приростом вектора називається приростом вектора  за час за час  (рис. 3.5). (рис. 3.5).
Величину Границя
З врахуванням (3.6) цю формулу можна записати так
 . .
Вектор прискорення руху матеріальної точки дорівнює похідній по часу від вектора швидкості і характеризує зміну швидкості з часом. Він завжди прикладений до матеріальної точки. Припустимо, що рух точки задано координатним способом
Позначивши через
Порівняємо відповідні координати в лівій і правій частинах
 ; ;  ; ; 
Аналогічно до (3.8), величина і напрямок вектора
 ; ;  ; ;  ; ;  , ,
де Якщо рух матеріальної точки задано натуральним способом, то
Позначимо через
Диференціюючи останню рівність по

Використаємо формулу Френе із курсу диференціальної геометрії
де
 . .
 Остання формула показує, що вектор прискорення розкладається на дві складові, одна з яких напрямлена вздовж дотичної до траєкторії і називається дотичним (тангенціальним) прискоренням Остання формула показує, що вектор прискорення розкладається на дві складові, одна з яких напрямлена вздовж дотичної до траєкторії і називається дотичним (тангенціальним) прискоренням 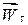 , а інша, яка напрямлена по головній нормалі, називається нормальним прискоренням , а інша, яка напрямлена по головній нормалі, називається нормальним прискоренням  (рис. 3.7) (рис. 3.7)
Величини цих складових і повного прискорення обчислюються за формулами
 ; ;  ; ; 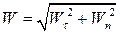 . .
Зауважимо, що при
Поиск по сайту: |
 . Розглянемо момент часу
. Розглянемо момент часу 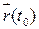 і точка
і точка 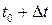 відповідає вектор
відповідає вектор  і точка
і точка  на траєкторії. Точки
на траєкторії. Точки  , який називається приростом вектора
, який називається приростом вектора 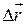 залежить від
залежить від  називається вектором середньої швидкості матеріальної точки за час
називається вектором середньої швидкості матеріальної точки за час 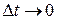 називається вектором миттєвої швидкості точки в момент часу
називається вектором миттєвої швидкості точки в момент часу  На підставі (3.6) можна зробити такий висновок: вектор швидкості руху матеріальної точки в довільний момент часу, дорівнює похідній від радіус-вектора точки в цей же момент часу і характеризує зміну положення точки відносно вибраної системи відліку з часом.
На підставі (3.6) можна зробити такий висновок: вектор швидкості руху матеріальної точки в довільний момент часу, дорівнює похідній від радіус-вектора точки в цей же момент часу і характеризує зміну положення точки відносно вибраної системи відліку з часом.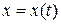 ;
;  ;
; 
 проекції вектора її швидкості
проекції вектора її швидкості 
 ;
; 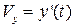 ;
; 
 які він утворює з координатними осями
які він утворює з координатними осями 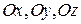 відповідно визначаємо за формулами векторної алгебри
відповідно визначаємо за формулами векторної алгебри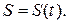
 .
.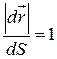 . Таким чином,
. Таким чином,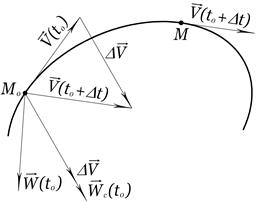 3.2.2. Прискорення точки. Швидкість руху матеріальної точки в кожен момент часу характеризує зміну положення точки відносно вибраної системи відліку. Разом з тим швидкість руху точки є функцією часу. Тому для повного кінематичного аналізу руху точки необхідно ввести ще одну кінематичну характеристику яка називається прискоренням.
3.2.2. Прискорення точки. Швидкість руху матеріальної точки в кожен момент часу характеризує зміну положення точки відносно вибраної системи відліку. Разом з тим швидкість руху точки є функцією часу. Тому для повного кінематичного аналізу руху точки необхідно ввести ще одну кінематичну характеристику яка називається прискоренням. .
.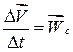 будемо називати вектором середнього прискорення за проміжок часу
будемо називати вектором середнього прискорення за проміжок часу 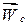 при
при 
 проекції на координатній осі прискорення
проекції на координатній осі прискорення  , на підставі (3.10) одержимо
, на підставі (3.10) одержимо .
.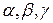 – кути, які утворює вектор
– кути, які утворює вектор  ;
;  .
. одиничний вектор дотичної до траєкторії в розглядуваній точці так, щоб виконувалася умова
одиничний вектор дотичної до траєкторії в розглядуваній точці так, щоб виконувалася умова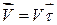 .
. одержимо
одержимо
 ,
, – радіус кривини траєкторії в розглядуваній точці;
– радіус кривини траєкторії в розглядуваній точці;  – вектор головної нормалі траєкторії, який перпендикулярний до
– вектор головної нормалі траєкторії, який перпендикулярний до  ;
;  .
.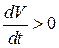
 , а при
, а при 
 .
.