Границы применимости классической механики

Механическое движение - это изменение взаимного расположе-

ния тел или их частей в пространстве. Совокупность тел, которая выде-

лена для рассмотрения, называется механической системой.

Изменение положения любого тела можно указать только по отно-

шению к некоторому другому телу. Для описания движения необходимо

так же определять время. Система тел, по отношению к которым рассмат-

ривается движение и отсчитывающее время часы называются системой

отсчета. Движение тела относительно различных систем отсчета имеет

разный характер. В этом смысле движение относительно. Например, ско-

рость и путь человека в движущемся поезде относительно вагона и отно-

сительно платформы разные.

Тело, размерами которого в условиях данной задачи можно прене-

бречь, называется материальной точкой или частицей (т.е. материальная

точка - математическая точка, имеющая массу тела). Материальная точка

- простейший объект механики. Очевидно, что материальная точка - это

простейшая модель тела, позволяющая упростить математическое описа-

ние движения. Другая простая модель тела - абсолютно твердое тело: это

тело, деформациями которого в условии данной задачи можно прене-

бречь. Абсолютно твердое тело можно представить как тело, состоящее из

огромного числа (теоретически - из бесконечного числа) материальных

точек, взаимное расположение между которыми не меняется при любых

условиях.

Механика состоит из нескольких разделов. Кинематика изучает

движение тел, не интересуясь причинами вызывающими это движение.

Типичная задача кинематики - зная начальные условия и характеристики

движения указать, где будет тело, и какова его скорость через любой про-

межуток времени. Динамика изучает движение тел в связи с причинами

(взаимодействием тел) которые вызывают это движение. Статика изучает

условия, при которых система остается в покое.

Все законы классической механики справедливы при скоростях

много меньших скорости света и для тел, масса которых много больше

массы атомов (следует обратить внимание на то обстоятельство, что ско-

рость света в классической механике ни в каких законах не фигурирует.

Теоретически это означает, что в классической механике скорость может

быть любой, в том числе и стремиться к ¥).

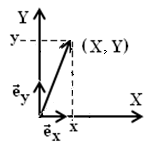
Радиус вектор, перемещение, траектория, путь.

Вектор скорости, модуль вектора скорости. Уравнение

Пути

Начнем изучение механики с механики материальной точки. Поло-

жение точки удобно задать в прямоугольной системе координат. Система

координат должна быть определенным, известным способом связана с

телами отсчета. Для простоты будем рассматривать плоское движение

(движение в плоскости), т.е. двумерную систему координат. Положение

точки определяется координатами xи y. Вектор проведенный из начала

координат в точку называется радиус-вектором точки (рис.2.1а). Из ри-

сунка 2.1а видно, что проекции вектора r на оси координат равны:

Рис.2.1б

r(t) = x(t)e_x + y(t)e_y

( В дальнейшем для упрощения орты на чертежах изображать не

будем). При движении точка “описывает” некоторую линию она называ-

ется траекторией (рис.2.1б). Длина траектории называется длиной пути

(или короче - путь). Вектор, соединяющий начальное положение точки

(положение в момент времени t₁ ) и конечное (в момент времени t₂ )

называется перемещением. На рисунке 2.1б это вектор Dr :

∆r = r(t₂ ) - r(t₁) = r₂ - r₁ = ∆xe_x + ∆ye_y

Средним вектором скорости v за время ∆t называется вектор рав-

ный:

r r r

υ = = (2.2)

Мгновенной скоростью называется величина равная

r Dr dr r

lim (2.3)

Dt®0

Таким образом, мгновенная скорость равна производной от радиус-

вектора по времени. Т.к. при ∆t®0 вектор ∆r стремится установиться

по направлению касательной (рис. (2.2)), то из (2.2) и (2.3) следует, что

вектор u направлен по касательной к траектории.

Подставим в (2.3) выражение (2.1)

υ = (xe_x + ye_y ) = e_x + e_y (2.4)

r

u_x,u_y,:

u =u_xe_x +u_ye_y (2.5)

Из сравнения уравнений (2.4) и (2.5)

видно, что проекции вектора скорости равны

соответствующим производным от коорди-

нат:

;

(2.6)

Найдем модуль вектора скорости, исходя из (2.3):

υ º υ =

∆t ∆t

Из рис. (2.2) видно, что модуль вектора Dr , т.е. его длина, стре-

миться к длине дуги траектории, которая “ограничивает“ вектор. Следо-

вательно, при ∆t®0 ∆r = ∆S , т.е. равен пути, которую проходит ча-

стица за время Dt. Таким образом, получаем:

υ = = = S (2.7)

∆t ®0

Модуль вектора скорости равен производной от пути по времени.

Модуль вектора скорости можно так же найти, зная его проекции

(рис. 2.3).

u = u_x +u_y

Выразим путь, предполагая, что

известна скорость u(t) (рис.2.3). Интер-

вал времени от t₁ до t₂ разобьем на ма-

лые промежутки ∆t_i. Тогда из (2.7) сле-

дует:

DS_i »u_iDt_i

∑^DSi∑^ui

Чем меньше все промежутки ∆t_i, тем точнее мы найдем путь:

t₂

∫^υ(t)dt(2.8)

t₁

Отметим, что уравнение (2.8) можно получить просто математиче-

ски из (2.7): dS = u(t) dt , проинтегрируем это равенство, считая, что

при t₁ S = 0, а при t₂ путь равен S:

S S

dS = dS = S , то получим уравнение (2.8)

0 t₁ 0

Из свойств интегралов следует, что путь равен площади под графи-

ком скорости.

Пример. Равномерным движением называется такое движение, при кото-

ром модуль скорости u постоянен (не меняется). Если u = const , то в ин-

теграле (2.8) u можно вынести за знак интеграла:

t₂

S = υ dt = υ(t)^t_t² = υ(t₂ - t₁ ) = υ∆t

( если t₂=t, а t₁=0 ⇒ S=ut).

Поиск по сайту: