Глава 3. Работа. Энергия

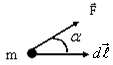
Работа. Работа при вращательном движении. Мощ-

Ность

r

Пусть к частице, массой m, приложена сила F_r, ча-

стица за время dt совершила перемещение d r . В

дальнейшем, вместо d r будем использовать обо-

значение dl ;(dl º dr).

Определение работы:

r r

dA = Fdl

работа равна скалярному произведению силы на перемещение.

Из свойств скалярного произведения следует

dA = Fdlcosa = F_ldl , (10.2)

Где F_l - проекция F на направление перемещения dl , a - угол между

векторами F и dl .

Из (10.2) ⇒

[A] = Нм = Дж (джоуль).

(Обратите внимание: т.к. dl величина ® 0, то можно считать, что на пе-

ремещении dl сила F = const).

Для того чтобы найти работу на всем пути надо весь путь разде-

лить на малые участки, найти работу на каждом из них, а затем результат

просуммировать. Таким образом, определение работы на всем пути сво-

дится к интегрированию (10.1) или (10.2)

∫ dA = ∫ Fdl = ∫ Fdl cosa = ∫ F_ldl . (10.3)

l l l l

Индекс «ℓ» в (10.3) означает, что суммирование (т.е. интегрирование)

проводится вдоль траектории обозначенной «ℓ». Интеграл слева в (10.3)

равен

∫ dA = A

l

∫ dA ¹ A₂ - A₁^{, т.к. работа в точке 2 и точке 1 смысла}

l

не имеет). Таким образом

(10.4)

l l

(в (10.4) написаны не все, а наиболее употребимые выражения для рабо-

ты). Сила в уравнении (10.4) может быть как одна из действующих на те-

ло сил (т.е. найдем работу этой силы) так и результирующая нескольких

сил (т.е. получим работу результирующей силы).

Пример:работа постоянной силы, частица двигается прямоли-

нейно: = const =>

A = ∫ F cosadl = F cosa ∫ dl = Flcosa

l l

Найдем работу при вращательном движении твердого тела вокруг

оси, не меняющей своей ориентации в пространстве. На рис. 10.2 показана

некоторая частица твердого тела, масса частицы m_i, за время dt частица

поворачивается на угол dj, который обозначим a: djºa. Работа совер-

шаемая над частицей равна:

dA_i=F_icosadS_i

F_i cosa = F_{t ,i} ⇒ dA_i = F_{t ,i}dl_i ; dl_i= R_idj ⇒ dA_i = F _{t ,i}R_idj

Множитель перед dj есть момент силы N_z,i (уравнение (8.9)):

dA_i=N_Z,idj (10.5)

Складывая работу, со-

вершаемую над каждой

из частиц, получим ра-

боту, совершаемую при

вращательном движении

тела

dA = ⇒

dA = dj N_{Z ,i} (10.6)

Сумма в правой части

(10.6) есть суммарный

момент внешних сил

∑

(10.7)

Работа, совершаемая при повороте тела на угол Dj, определяется инте-

грированием уравнения (10.7):

Dj

(10.8).

0

Мощность Р - это работа совершаемая в единицу времени:

dA

(10.9)

dt

Р=Дж/с=Вт (Ватт)

Подставим в (10.9) уравнение (10.1):

P = ;

С учетом (2.1), получим:

P = Fu (10.10)

Для вращательного движения из формул (10.7) и (10.9) следует, что

P=N_Zw

Работа и кинетическая энергия. Кинетическая