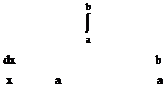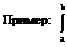Для дальнейшего отметим, что в физике производные не принято

Обозначать значком «штрих: у’». Есть специальные обозначения

только для функции времени. Если z = f (t) , то производная по времени

обозначается следующим образом: z = (= z').

2

Вторая производная: .

1.17. Производные: постоянной, произведения постоянной на функцию,

суммы (разности), произведения, частного.

А. Производная от постоянной величины равна 0, т.е. если y = c, где

с = const , то y’=0

Б. Постоянный множитель можно вынести за знак производной, т.е. если

y = cu (x), где c = const, то y’=c×u’(x).

В. Производная от суммы (разности) функций равна соответствующей

сумме (разности) производных этих функций, т.е. если

y = u(x)+ v(x)+ w(x) , то” y = u (x) + v (x) + w (x).

Г. Если y = u(x)×v(x) , то” y = u (x)×v(x) + u(x)×v (x)

u(x) u (x) × v(x) - u(x) × v (x)

v(x)

1.18. Некоторые табличные производные:

(xⁿ ) = nx^n-1 , (e^x ) = e^x , (a ) = a ln a

, (cos x) = -sinx , (sinx) = cosx

	cos2 x
		¢

, (ctgx) = -

Если a = const , то (cosax) = -asinax , (sinax) = acosax.

1.19. Частная производная. Если z есть функция двух переменных x и y,

то частной производной по x от функции z = f (x, y) называется произ-

водная по x , вычисленная в предположении, что y есть постоянная вели-

чина. Аналогично определяется частная производная по y.

z = x y³ , то” = 2xy³ , = 3x²y²

1.20. Дифференциал функции.

Если , где dy - дифференциал функции

y = f (x) – т.е. бесконечно малое приращение функции при бесконечно

малом приращение аргумента.

S » Dx_i - площадь ограниче-

ния кривой y(x) на участке от a до b.

S = Dx_i ⇒

Dx_i ®0

это есть интеграл

Первообразная F(x) для функции

y(x):

b

y(x)dx = F(x) = F(b) - F(a)

b

= ln x = ln b - ln a = ln

1.22. Интеграл от суммы (разности) функции равен сумме (разности) ин-

тегралов, т.е.

∫^{[f (x) + f2 (x) - f3(x)]× dx =} ∫^{f (x)dx +} ∫^{f (x)dx -} ∫^{f (x)dx}

Постоянный множитель можно выносить за знак интеграла, т.е.

c × f (x)dx = c_∫ f (x)dx , где с - постоянная величина.

Некоторые табличные интегралы.

∫^{dx = x + const ;} ∫

n+1

x dx = + const; где n¹-1;

n + 1

∫^{e dx = ex + const}

∫^{cos x × dx = sin x + const ;} ∫^{sin x × dx = - cos x + const}

Глава 1. Кинематика.

Механическое движение. Система отсчета.

Материальная точка. Абсолютно твердое тело.

Поиск по сайту: