 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
IV. Дифференциальное исчисление
Производная функции Производной функции f(x) в точке x0 называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует и конечен.
Справедливы следующие правила:
Нахождение производной называется дифференцированием функции. Основные формулы дифференцирования:
Пример 1. Найти значение производной функции f(x) в точке если Решение. Функция f(x) представляет собой алгебраическую сумму двух функций:
Следовательно: Функция p(x) есть композиция логарифмической и тригонометрической функций, а значит, по правилу 5 Функция q(x) есть композиция степенной и тригонометрической функций, следовательно, по правилам 1, 5
Таким образом:
при Ответ: Пример 2. Найти значение производной функции f(x) в точке x0 = 2, если Решение: Функция f(x) представляет собой произведение двух функций: Следовательно, по правилу 3 Согласно правилу 2, Функция q(x) есть композиция функций: логарифмической и линейной, так как
При преобразовании функции q(x) были использованы свойства степени и свойства логарифма. Таким образом:
по правилам 1, 5. Найдем
При x0 = 2
Ответ:
Производные высших порядков функции Производная f'(x) называется производной первого порядка от функции f(x). Производная (f'(x))' называется производной второго порядка от функции f(x). Обозначение: fII(x). (fII(x))' = fIII(x) – производная третьего порядка от f(x). (fIII(x))' = fIV(x) – производная четвертого порядка от f(x) и т. д. Если f(n–1)(x) – производная (n – 1) порядка функции от f(x), то (f(n–1)(x))' = f(n)(x) – производная n-го порядка от f(x). Пример 3. Найти производную третьего порядка от функции f(x) = cos2x. Решение:
Ответ:
V. Интегральное исчисление
Понятие неопределенного интеграла и его свойства Функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для всех точек этого промежутка выполняется равенство F'(x) = f(x). Если F(x) – первообразная для функции f(x) и С – некоторая постоянная, то (F(x) + C) также есть первообразная для f(x). Неопределенным интегралом от функции f(x) называется множество функций (F(x) + C), являющихся первообразными для f(x). Обозначение:
Основные свойства определенного интеграла:
Таблица основных интегралов
Методы интегрирования
5.3.1. Непосредственное интегрирование. Нахождение интегралов с помощью таблицы интегралов и основных свойств интеграла
Пример 1. Найти интеграл: Решение: Согласно свойствам 1, 2, 3 интеграл примет вид:
По таблице интегралов находим:
Следовательно,
Обычно сумму всех неопределенных постоянных обозначают одной буквой: Пример 2. Найти интеграл Решение: Рассмотрим подынтегральную функцию Согласно свойству 4 и формуле (1) таблицы интегралов, определяется интеграл:
5.3.2. Метод замены переменной
При нахождении интегралов вводится новая переменная, с помощью которой значительно упрощаются подынтегральные функции и интегралы принимают табличный вид. Определив интеграл по новой переменной, обратной подстановкой возвращаются к исходной переменной. Пример 3. Найти интеграл Решение. Интеграл является нетабличным. Выполним замену переменной:
Таким образом, подынтегральная функция по переменной у имеет упрощенный вид, а интеграл сводится к табличному интегралу:
Возвращаясь к переменной х, имеем:
Следовательно:
Поиск по сайту: |

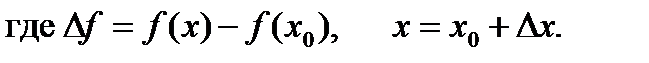


 ,
, .
.
 по правилу 2.
по правилу 2.


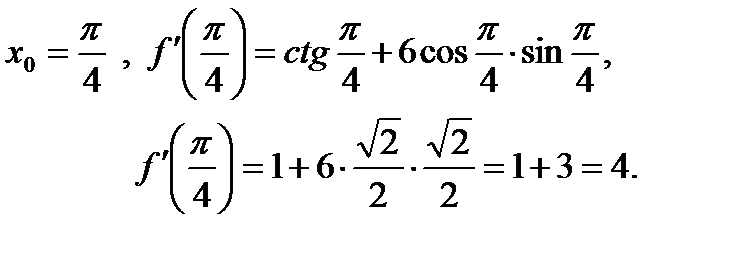
 .
. .
. .
. .
. .
.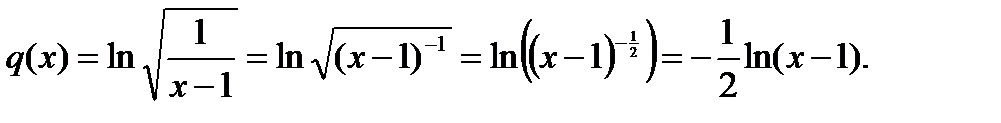
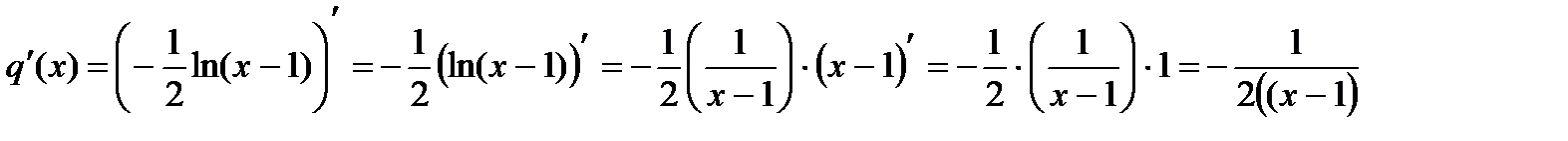
 :
:
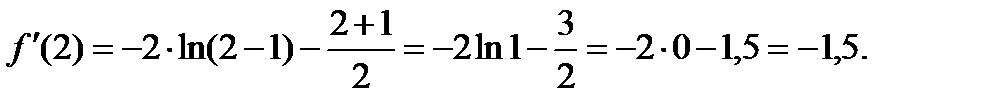

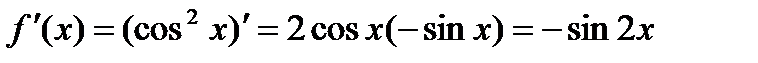 (правило 5).
(правило 5). (правило 5).
(правило 5).



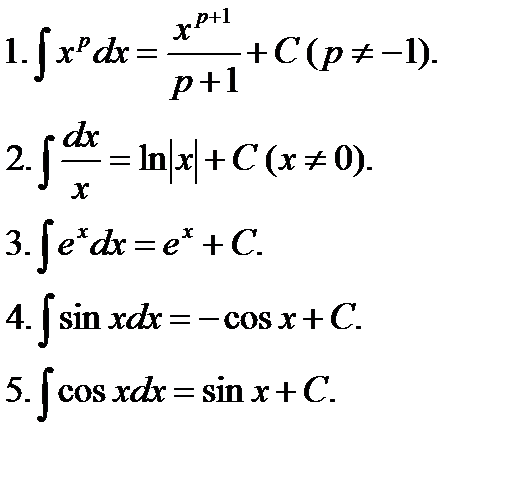
 .
.


 .
. . Представим ее в виде композиции двух функций: степенной и линейной
. Представим ее в виде композиции двух функций: степенной и линейной  .
.
 .
.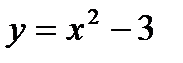 .Найдем дифференциалы от левой и правой частей равенства и выразим из него xdx.
.Найдем дифференциалы от левой и правой частей равенства и выразим из него xdx.
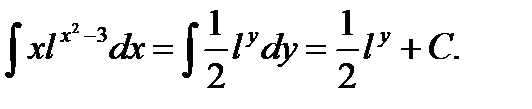

 .
.