 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Разложение определителя по элементам строки или столбца
Миноромэлемента aij определителя D называется определитель второго порядка, полученный из данного вычеркиванием×строки и столбца, содержащих взятый элемент. Обозначение: Mij.
Пример.
Алгебраическим дополнением элемента аij называется минор этого элемента, умноженный на коэффициент (–1)i+j. Обозначение: Аij = (–1)i+j × Mij.
Пример.
Теорема: Если
или
Пример.Вычислить определитель разложением по элементам:
Решение: 1) i =2,
2) i = 3,
Ответ:
Решение систем линейных уравнений методом определителей (метод Крамера) Рассмотрим систему трех линейных уравнений с тремя неизвестными: x1, x2, x3:
(коэффициенты aij и свободные члены bi считаются заданными). Решение: составим определители
где D называют определителем системы, а определители Dxi получены из основного определителя D заменой свободными членами bi элементов соответствующего столбца.
Особые случаи: 1) если D ¹ 0, то система имеет единственное решение; 2) если D = 0, Dxi ¹ 0, то система несовместна; 3) если D = Dxi = 0, то система либо имеет бесконечное множество решений, либо она решений не имеет. Пример. Решить систему линейных уравнений: Решение: составим определители D, Dx, Dy, Dz и найдем их значения.
Найдем решение системы: Ответ: (3; 2; –1).
II. Аналитическая геометрия Координаты вектора в пространстве. Действия над векторами в координатной форме
Выберем:
Всякий вектор пространства можно представить в виде линейной комбинации единичных векторов
где Длина вектора Рассмотрим две точки пространства: Найдем координаты вектора
Таким образом, Длина вектора Справедливо следующее утверждение:
Пример 1. Найти расстояние между точками А и В, если известно, что А(–2;3;1) и В(2;1;5). Решение: 1. Найдем координаты вектора
2. Вычислим длину вектора Ответ: 6.
Пример 2. Найти длину вектора Решение: 1. Обозначим: 2. Найдем координаты вектора 3. Найдем координаты вектора 4. Вычислим длину вектора Ответ: 3.
Поиск по сайту: |
 – минор элемента а12.
– минор элемента а12. – минор элемента а33.
– минор элемента а33. .
. .
. , то
, то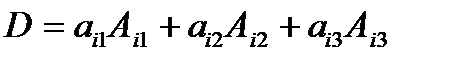 , где i – номер строки,
, где i – номер строки, , где j – номер столбца.
, где j – номер столбца.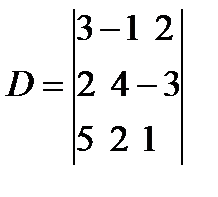
 1) второй строки; 2) третьего столбца.
1) второй строки; 2) третьего столбца. .
. .
. .
. .
. .
. .
. .
. .
. .
.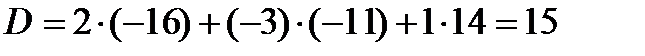 .
.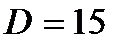 .
.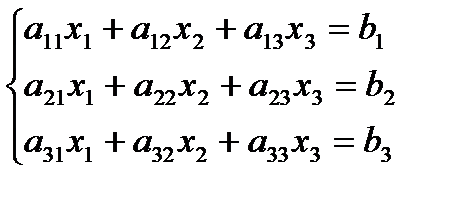

 :
: ,
,  ,
,  ,
,  ,
,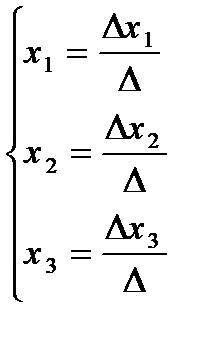

 (D ¹ 0, следовательно, система имеет единственное решение).
(D ¹ 0, следовательно, система имеет единственное решение). .
. .
. .
.

 Пусть M(x; у; z) – координаты точки в пространстве.
Пусть M(x; у; z) – координаты точки в пространстве. – единичные векторы на соответствующих осях координат:
– единичные векторы на соответствующих осях координат:
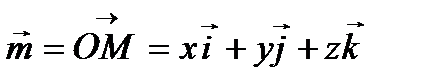 ,
, – координаты вектора в пространстве.
– координаты вектора в пространстве. вычисляется по формуле
вычисляется по формуле  .
. и
и 
 :
:  .
.
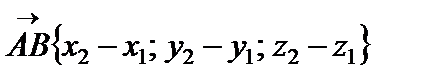 – координаты вектора
– координаты вектора 
 определяется по формуле
определяется по формуле  .
. пусть:
пусть:  и
и  тогда
тогда

 .
.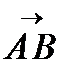 :
: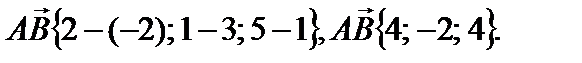

 если
если  .
.




