 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вычисление погрешностей прямых измерений
Представим, что мы на опыте измерили какую-либо величину и получили всего «m» результатов отдельных измерений: N1, N2, N3…Nn –всего «n» измерений. По сказанному выше – среднее арифметическое будет наиболее близким к истинному значению измеряемой величины:
Будем называть величину N средним арифметическим или, с некоторым приближением, истинным значением искомой величины. Найдем разницу между отдельным каждым измерением и истинным значением измеряемой величины, т.е. N - N1 = ±∆N1 N - N2 = ±∆N2 …………… N - Nn = ±∆Nn. Берем знаки ±, т.к.Ni могут быть как больше, так и меньше N. Разность между истинным значением измеряемой величины и отдельным измерением дает нам абсолютную погрешность отдельного измерения. Среднее арифметическое из численных значений отдельных ошибок называется средней абсолютной ошибкой измерений: (абсолютные ошибки берутся по абсолютной величине)
Зная абсолютные погрешности отдельных измерений, можно найти относительные ошибки отдельных измерений, которые представляют собой отношение следующих величин:
Относительные погрешности выражаются обычно в %, в то время как абсолютные – в единицах измерения искомой величины. Отношение средней абсолютной ошибки ∆N к среднему арифметическому N называется средней относительной ошибкой измерения: Например: 1. Измерение времени:
Е = Искомый результат записывается: t = (19,9±0,2) с. 2. Измерение толщины пластинки:
Отсюда видно, что абсолютная погрешность показывает, в каких пределах находится измеряемая величина. По абсолютной погрешности можно судить и о точности измерения однородных величин одного порядка. Например,
второе измерение сделано с точностью в 10 раз большей, чем первое. Относительная же погрешность позволяет судить о степени точности измерения величин разных порядков как однородных, так и разнородных. Поясним это примером: были измерены две физические величины – толщина пластинки d и скорость света c. С учетом абсолютных ошибок измерения эти величины запишутся: d ± ∆d = (2,25 ± 0,01) мм, с ± ∆с = (300000 ± 100) км/с. На первый взгляд (по абсолютным ошибкам измерения) кажется, что толщина пластинки измерена точнее скорости света. Но! Значение ∆d и ∆с не позволяет судить о степени точности этих измерений. Найдем относительные погрешности:
откуда следует, что второе измерение было произведено с точностью, примерно в 10 раз большей, чем первое, что с первого взгляда было неочевидно. В том случае, когда данная физическая величина определялась много раз – теоретически число измерений равно ∞ - степень точности результата измерений можно оценить более строго, воспользовавшись формулой, которую дает теория вероятностей. Это так называемая средняя квадратичная абсолютная погрешность: Здесь n – число измерений, а ∑(∆Ni)2 есть сумма квадратов абсолютных ошибок отдельных измерений.
Поиск по сайту: |
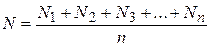
 .
.

 или в процентах Е=1 %.
или в процентах Е=1 %. , d = (2,24±0,03) мм.
, d = (2,24±0,03) мм. 1 = 25 см;
1 = 25 см;  1 = 0,1 см и
1 = 0,1 см и
