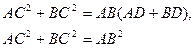|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сто доведень теореми Піфагора ⇐ ПредыдущаяСтр 10 из 10
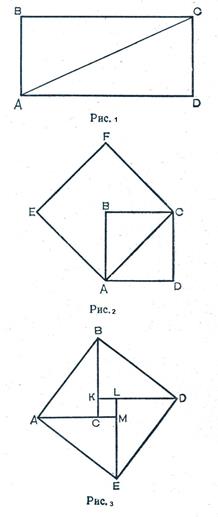
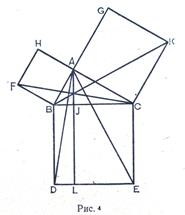
Ще одне доведення теореми Піфагора викладено Евклідом в «Началах». Як формуліровка, так і доведення мають у Евкліда чисто геометричний характер. На гіпотенузі і катетах прямокутного трикутника ВАС (рис.4) побудовано відповідні квадрати і доводиться, що квадрат, побудований на гіпотенузі, рівновеликий сумі квадратів, побудованих на катетах.
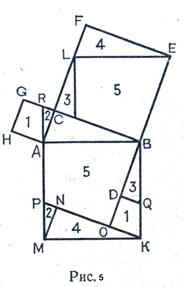
Більшість із даних після Евкліда доведень теореми Піфагора основані на тому, що рівно складені фігури рівновеликі: квадрати. Побудовані на катетах і гіпотенузі, розбиваються на многокутники так, що кожному многокутнику із скаду квадрата на гіпотенузі відповідає рівний многокутник одного із квадратів на катетах. В таких випадках досить подивитися на малюнок. Щоб зрозуміти усе доведення. Багдадський математик та астроном Х ст.Анарицій дав таке доведення – (рис. 5)
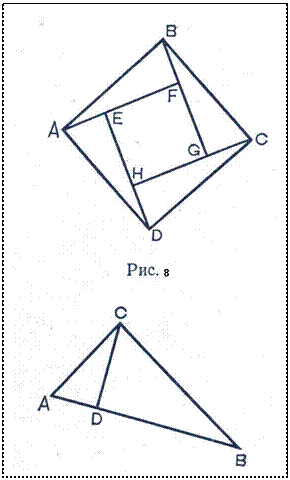
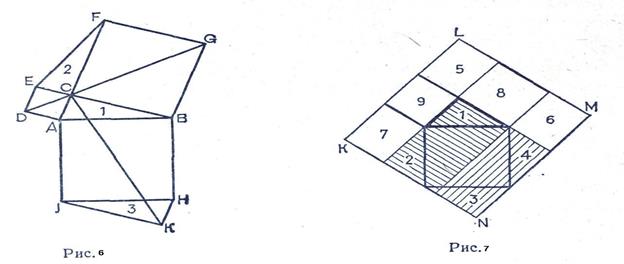
Інші доведення основані на тому,що, додаючи до квадратів на катетах і до квадрату на гіпотенузі рівні фігури, отримуємо рівновеликі фігури. Наприклад на рисунку 6 до Піфагорової фігури добавлені трикутники 2 і3, рівні даному трикутнику 1. Доведення теореми Піфагора зводиться до доведення рівновеликості шестикутників DABGFE і CAJKHB. Останнє видно з того, що пряма DG ділить пополам перший , пряма СК – другий шестикутник. А якщо повернути половину першого шестикутника DABG навколо точки А на 90°, то вона співпаде з САJK, половиною другого шестикутника. Ще одне доведення (рис. 7). Тут Піфагорові фігура достроєна до прямокутника KLMN. Віднімаючи многокутники 1; 2; 3; 4; 5; 6; 7; 8; 9, отримуємо квадрат, побудований на гіпотенузі, а віднімаючи від того ж прямокутника фігури, рівновеликі тільки що переліченим (5; 6; 7 і зафарбовані прямокутники), отримуємо квадрати 8 і 9, побудовані на катетах, і доводимо, що площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів 8 і 9.
У давнину теорему Піфагора називали «віслючим мостом». Це тому, що учнів, які завчили теорему напам’ять, але не розуміли її, називали віслюками – для них вона була ніби непрохідним мостом. Також теорему Піфагора учні називали «вітряним млином». Про теорему складали вірші такі як: Пифагоровы штаны Во все стороны равны, малювали карикатури.
Задачі 1)Задача Брахмагупти Знаючи висоту свічки та висоту вертикальної жердини, а також відстань між ними, знайти довжину тіні жердини 2).Задача з «Книги абака» Л. Пізанського (Фібоначчі). Дві башні, одна висотою 40 футів, а друга – 30 футів, розташовані на відстані 50 футів одна від одної. До розташованої між ними криниці злітаються одночасно з обох башен дві птички і, пролітаючи з однаковою швидкістю, одночасно прибувають до криниці. Знайти відстань криниці від башен 3) Теорема Ейлера В будь-якому чотирикутнику сума квадратів сторін дорівнює сумі квадратів його діагоналей, складеної з учетверенних квадратом відрізка, який з’єднує середини діагоналей. Задача о лотосе Над озером тихим С полфута раз мером Высится лотоса цвіт. Он рос одиноко, И ветер поривом Отес его в ссторону. Нет Боле цветка над водой Нашел жн рыбак его Ранней весною В двух футах от места,где рос. Итак, предложу я вопрос: Как озера вода здесь глибока? Задача про тополю На березі річки тополя росла, І вітру порив її стовбур зламав. Тополя упала, і стовбур її Кут прямий з течією ріки утворив. Пам’ятай: в тому місці ріка Три фути була шириною. Верхівка зхилилась до краю, Залишивши три фути всього над водою. Прошу, тепер швидше скажи мені ти: Тополя , якої була висоти? 7) - Скажи мені славетний Піфагоре, скільки учнів відвідують твою школу і слухають твої бесіди? - Ось скільки, - відповів філософ: - половина вивчає математику, чверть – музику, сьома частина перебуває в мовчанні і, крім того, є ще три жінки. Скільки ж учнів було в школі Піфагора?
Література 1. Коменський Я. А. Велика дидактика. – К.,1940. (1; с. 114,125,126) 2. Коменський Я. А. Избранные педагогические сочинения. – М.: Педагогика, 1982.- (Т. 1; с. 176, 304) 3. Лизинский В. М. Приемы и формы учебной деятельности. – М.: Центр «Педагогический поиск», 2002 4. Освітні технології: Навч. – метод. посіб. / О.М. Пєхота, А.З. Кіктенко, О. М. Любарська та ін.; За заг. ред. О.М. Пєхоти. – К.:А.С.К., 2001 5. Сиротинко Г.О. Сучасний урок: інтерактивні технології навчання. – Х.: Видав. гр. «Основа» , 2003 6. Дидактичні ігри на уроках математики. 5-6 класи / Уклад. І. С. Маркова. – Х.: Видав. гр. «Основа», 2006 7. Булатова О. С. Искусство современного урока. – М., 2006 8. Русаков, Андрій Епоха великих відкриттів у школі 90-х років. – К.: Вид. дім «Шкільний світ»:Вид. Л. Галіцина, 2006 9. Капіносов А., Гаук М., Кондратьєва Л. Математика. 5 клас. Дидактичні матеріали для тематичних атестацій з математики. – Тернопіль: Підручники і посібники, 2003. 10. Капіносов А., Математика. 6 клас. Дидактичні матеріали для тематичних атестацій з математики. – Тернопіль: Підручники і посібники, 2003. 11. Капіносов А., Геометрія 7 клас. Посібник для рівневого навчання з геометрії. Ч.І. Навчальні завдання. – Тернопіль: Підручники і посібники, 2004. 12. Сухарева Л. С. Завдання для усної роботи, математичні диктанти та тести. Геометрія. 10 – 11 клас. – Х. : Видав. гр. «Основа» , 2008 13. Мерзляк А. Г. , Полонський В. Б. , Якір М. С. Математика . 5 клас: Підручник. – Х.: Гімназія , 2005. 14. Мерзляк А. Г. , Полонський В. Б. , Якір М. С. Математика . 6 клас: Підручник. – Х.: Гімназія , 2006. 15. Мерзляк А. Г. , Полонський В. Б. , Якір М. С. Математика . 5 клас: Книга для вчителя. – Х.: Гімназія , 2005. 16. Мерзляк А. Г. , Полонський В. Б. , Якір М. С. Математика . 6 клас: Книга для вчителя. – Х.: Гімназія , 2006. 17. Мерзляк А. Г. , Полонський В. Б. , Якір М. С. Математика . 5 клас: Робочий зошит. – Х.: Гімназія , 2005. 18. Мерзляк А. Г. , Полонський В. Б. , Якір М. С. Математика . 6 клас: Робочий зошит. – Х.: Гімназія , 2006. 19. Беденко В. М. Цифра, цифра, кома…: Зошит з друкованою основою. – К.: А.С.К., 1996. 20. Погорєлов О.В. Геометрія : Планіметрія: Підручник для 7-9 кл. серед. шк. – К.: Освіта, 1994. 21. Погорєлов О.В. Геометрія : Стереометрія: Підручник для 10-11 кл. серед. шк. – 4-те вид. - К.: Освіта, 1998-2003. 22. Прасолов В.В. , Шарыгин И.Ф., Задачи по стереометри. М.: Наука. Гл. ред. физ-мат. лит. , 1989. 23. Роєва Т.Г. , Синельник Л. Я. Математика в таблицях . 5-6 клас% Навч. посібник . – Х.: Видавнича група «Академія», 2002. 24. Інтерактивні технології на уроках математики /Упорядник І.С. Маркова. – Х.: Видавн. гр. «Основа», 2007. 25. Федь А. М. Эстетическое воспитание на урокх по основам наук. – к.: Рад. школа, 1984. 26. Кравчук Василь, Янченко Галина Алгебра. Підручник для 7 класу./ За редакцією Слєпкань З. І. Видання друге, перероблене та доповнене. – Тернопіль: Підручники і посібники, 2003. 27. Глейзер И.Г. История математики в школе VІІ – VІІІ Кл. Пособие для учителей. – М.: Просвещение, 1982.
Поиск по сайту: |
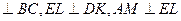 , тоді
∆АВС=∆ВDК=∆DEL=∆AME. Тому KL=CM=LM=
=CK=a-b.
Отже,
, тоді
∆АВС=∆ВDК=∆DEL=∆AME. Тому KL=CM=LM=
=CK=a-b.
Отже, 
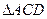 ~ ∆САВ, тому
~ ∆САВ, тому 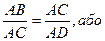
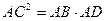 (1).
∆АВС ~ ∆DCB, тому
(1).
∆АВС ~ ∆DCB, тому  , або
, або
 (2).
Додавши (1) рівність та (2), отримаємо:
(2).
Додавши (1) рівність та (2), отримаємо: