ІІІ. Вивчення нового матеріалу. На дошці вивішено таблицю із зображенням прямокутних трикутників.

На дошці вивішено таблицю із зображенням прямокутних трикутників.

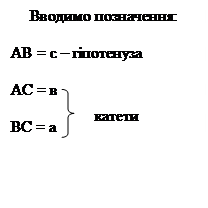
1. Назвати в кожному трикутнику

а). гострі кути, катети, гіпотенузу;

б). прилеглий катет до гострого кута;

в). протилежний катет до гострого кута.

Вводимо поняття косинуса кута.

Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи.

Позначається cos A.

На дошці записуємо вирази для cos A і cos В.

Учні в зошитах записують вирази для cos М, cos N, cos Е, cos Т, cosS, cos Р, cos Д самостійно.

Відповіді перевіряються.

Усні вправи

Знайди косинуси кутів за готовими малюнками.

Результати задачі № 4 бажано записати на дошці.

Це дасть змогу учням зробити висновки:

1. Значення косинуса кута А в трьох різних трикутниках одне і те ж саме, тобто не залежить від розмірів трикутника і розташування трикутників.

2. Якщо в прямокутних трикутниках гострі кути рівні, то косинуси цих кутів рівні.

Ці висновки дають можливість сформулювати теорему:

Т. Косинус кута залежить

від градусної міри кута

і не залежить від розміщення

і розмірів трикутника.

Далі учням пропонується відкрити підручник (п. 62, стор. 97. геометрія 7-9. Погорєлов) самостійно опрацювати доведення за підручником і скласти план доведення теореми, який потім записується на дошці. Сильному учню можна запропонувати за готовим планом довести теорему.

		С1

План

1. Додаткова побудова АВ₁С₁ = А¹ В¹ С¹

2. Довести, що ВС || В₁ С₁

3. Скористатися теоремою про пропорційні відрізки і записати пропорцію.

4. Скористатися тим, що за побудовою

АС₁ = А¹ С¹, АВ₁ = А¹ В₁

і зробити висновки.

Задачі на закріплення

1. Накреслити довільний прямокутний трикутник. Виміряти його сторони ы знайти косинус кожного гострого кута.

2. Знайти косинуси кутів прямокутного трикутника зі сторонами:

(Задачу № 2 можна запропонувати виконати 2 учням біля дошки в той час, коли весь клас виконує практичну роботу).

3. Що можна сказати про величину косинуса гострого кута?

(Відповідь: cosА < 1).

4. Побудувати кут А, якщо: cos А = . (Задачу № 4 виконати з поясненням на дошці).

Далі вводяться аналогічно поняття : sinА, tgА, ctg А і записуються такі формули:

Робимо висновки: 1). У АВС (С = 90^о)

cos А = sin В tg А = ctgB

cos В = sin А tg В = ctgA

Закріплення понять відбувається за готовими малюнками:

		N

	С			S

2). Радіус кола 10 см. Знайти косинус кута між діаметром АВ ы хордою АС, довжина якої 14 см.

Поиск по сайту: