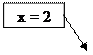|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Клас. Тема «Скорочення дробів»
На початку вивчення теми проводжу з учнями бесіду: уяви, що ти директор підприємства, на якому працюють четверо інженерів, троє секретарів, два економісти і один бухгалтер. Треба скоротити штати за рахунок однакових посад. Кого б ти скоротив? Після того як учні впорались із завданням, продовжуємо бесіду далі: уяви, що ти директор підприємства, а штат твоїх підлеглих – дроби:
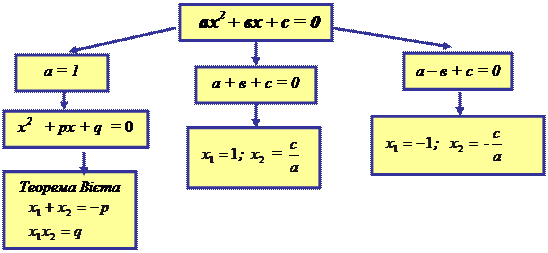
Використовуючи основну властивість дробу, учні скорочують «штати» і формулюють правило скорочення дробів. Спираючись на сучасні досягнення психолого-педагогічної теорії, творчо переосмислюючи і розвиваючи їх, віддаю перевагу груповим формам роботи, роботі в парі і творчій самостійній роботі учнів. Поєдную фронтальну, групову та індивідуальну роботу, враховуючи навчально-виховну мету уроку, зміст навчального матеріалу, рівень підготовки класу та окремих учнів. Групову роботу застосовую як на уроках формування умінь і навичок, узагальнення та систематизації знань, так і на уроках засвоєння нового матеріалу.Це ефективно сприяє формуванню знань, навичок і вмінь, створенню атмосфери співпраці, взаємодії. Наприклад, на уроці розвитку навичок обчислень або використання знань треба якомога більше розв’язувати однотипних, а потім і різноманітних прикладів, задач. На таких уроках намагаюсь використовувати різнорівневі картки, перфокартки, роботу по групах, конкурси, змагання команд, дидактичні ігри тощо. Також при проведенні таких уроків використовую самооцінку та взаємо-перевірку. Таким чином досягається підвищення відповідальності учнів за власні успіхи. Уроки контролюючого характеру намагаюся проводити за кількома різнорівневими варіантами. Самостійні та контрольні роботи, математичні диктанти, практичні роботи наряду з обов’язковою частиною мають також набір додаткових завдань, які дають можливість кожному учневі працювати на тому рівні складності, який йому по силі. А ось уроки, направлені на осмислення оптимальних знань, проводжу з використанням узагальнюючих схем і таблиць, алгоритмів розв’язань. Наприклад, при вивчені теми “Квадратні рівняння”, на дошці поступово з’являються схеми-таблиці:
=0
“Особливі випадки” розв’язування квадратних рівнянь
Або при вивчені теми “Системи лінійних рівнянь з двома невідомими” пропоную виділяти по ходу головні кроки розв’язку. Наприклад:
Із сильнішими учнями розглядаю у загальному вигляді. Це дає змогу кожному учневі з перших кроків приводити в систему свої знання, тим паче учням подобаються логічні варіанти. І, нарешті, уроки ознайомлення з новим дуже скурпульозно продумую. Вони головні в розвитку пізнавальної активності учнів. Тут йде у хід усе, особливо наочність, простота і доступність у розкритті змісту уроку. На цих уроках намагаюся проводити практично-дослідницьку роботу. Ця робота приводить учнів до висновку, а потім вони це твердження доводять.
Поиск по сайту: |
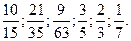 Треба скоротити «штати» за рахунок «однакових посад». Чи міг би ти це зробити?
Треба скоротити «штати» за рахунок «однакових посад». Чи міг би ти це зробити?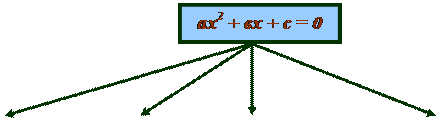
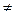 0
D =b2-4ac
D<0
не має коренів
D=0
х =
0
D =b2-4ac
D<0
не має коренів
D=0
х =  D>0
х1 =
D>0
х1 = 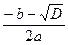 х2 =
х2 = 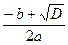
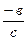


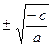 нів
нів




 +
+ 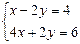


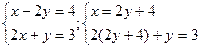 2 (2у + 4) + у = 3
4у + 8 + у = 3
5у = - 5
2 (2у + 4) + у = 3
4у + 8 + у = 3
5у = - 5