|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
І. Актуалізація опорних знань
1. Перевірка домашнього завдання:
а). № 2(1); № 3(2); № 4; № 6(1) – у формі усного рахунку (за готовими малюнками):
б). № 10 № 11 (Ці задачі біля дошки готують двоє учнів)
в). Доведення теореми Піфагора. Двоє учнів готують біля дошки: один – доведення за пунктом підручника, а другий – приводить своє доведення, яке вдалося знайти в додатковій літературі. г). Робота в парах (до 10 хвилин). На кожній парті є конверт з завданнями (теоретичні). Один учень виступає у ролі вчителя і слухає відповіді свого сусіда по парті. Фіксує кількість правильних відповідей, якщо необхідно, допомагає сусіду знайти правильну відповідь). Потім міняються ролями. Вчитель підходить до кожної пари, щоб мати уявлення про теоретичне знання учнів з теми.
Запитання до карток 1. Що називається косинусом кута? 2. Від чого залежить косинус кута? 3. Що можна сказати про значення косинуса, якщо порівняти його з одиницею? 4. Що називається синусом кута? 5. Від чого залежить синус кута? 6. Що можна сказати про значення синуса, якщо порівняти його з одиницею? 7. Що називається тангенсом кута? 8. Від чого залежить тангенс кута? 9. Сформулювати теорему Піфагора. 10. Як називають трикутник із сторонами 3, 4, 5.
ІІ. Вивчення нового матеріалу (у вигляді фронтальної бесіди). 1. Порівняйте катети прямокутного трикутника з його гіпотенузою. Зробіть висновок. 2. Чи може косинус гострого кута бути рівним одиниці або бути більшим за одиницю? 3. Побудуйте пряму а і позначте точку М, яка не лежить на ній. Проведіть до прямої з точки М перпендикуляр, та три довільні похилі, дві з яких рівні.
а
4. Порівняйте похилі з перпендикуляром. 5. Що можна сказати про проекції рівних похилих? 6. Що можна сказати про похилі, якщо їх проекції рівні? 7. Порівняйте проекції двох нерівних похилих. 8. Порівняти дві похилі, якщо проекція першої похилої більша від проекції другої похилої.
ІІІ. Розв’язування задач. 1. Усні вправи на закріплення наслідків з теореми.
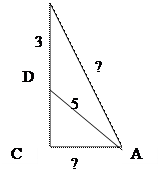
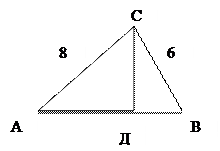
Катети прямокутного трикутника дорівнюють 6 і 8 см. Знайти проекції катетів на гіпотенузу.
(Цю задачу потрібно розв’язати колективно).
Розв’язування
АВ2 = АС2 + ВС2 АВ = АС2 + ВС2
АВ = 82 + 62 = 100 = 10 (см)
З ∆ ВСД : СD2 = АС2 – АD2, тоді АС2 – АD2 = ВС2 – ВD2
82 – Х2 = 62 – (10 – Х)2 64 – Х2 = 36 – 100 + 20 Х – Х2 20 Х = 128 Х = 6,4 (см)
10 – 6,4 = 3,6 (см) АD = 6,4 см, ВD = 3,6 см
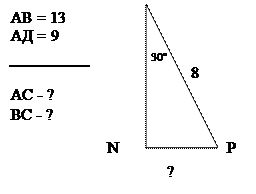
Задача № 4 З точки, що знаходиться на відстані 10 см від прямої, проведено дві похилі, довжини яких дорівнюють 26 см і 20 см. Знайти відстань між основами похилих. Скільки розв’язків має задача? (Зробити на дошці малюнок до даної задачі. Після того, як з’ясується, що можна зробити 2 різних малюнка до цієї умови, то запропонувати учням зробити цю задачу по варіантам).
ІV. Підсумок уроку 1. Сформулюйте наслідки з теореми Піфагора.
V. Домашнє завдання 1. Вивчити п. 63 (до кінця) п. 65 2. А № 18 ст. 107 Б № 19 ст. 107 В Довести, що відношення квадратів катетів дорівнює відношенню їх проекцій на гіпотенузу.
Урок 5 Тема:Терема Піфагора. Наслідки з тереми Піфагора Мета:Формувати вміння розв’язувати задачі, використовувати теорему Піфагора і наслідки з неї; продовжити формувати навички розв’язувати квадратні рівняння, розвивати навички робити відкриття. Хід уроку
А задачу (В) перевірити в класі і зробити деякі висновки.
Доведення
1. При доведенні теореми Піфагора були отримані вирази:
АС2 = АВ · АD ВС2 = АВ · ВD
2. Знайдемо відношення АС2 до ВС2
АС2 = АВ · АD АD – проекція катета АС на гіпотенузу АВ.
Висновок: квадрат катета прямокутного трикутника дорівнюють добутку гіпотенузи і проекцію цього катета на гіпотенузу.
ІІ. Актуалізація опорних знань
ІІІ. Учні виконують самостійну роботу
Завдання: № 1 – 3 Завдання обов’язкового рівня № 4 – 5 Завдання достатнього рівня № 6 Завдання високого рівня
Щоб отримати високий бал, виконуються завдання № 4 – 6.
Поиск по сайту: |




 АС
АС
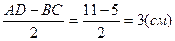
 АF =
АF =  АF =
АF = 
 ВD =
ВD = 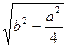 ВD =
ВD = 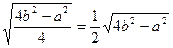









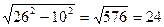


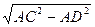 СD =
СD = 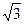 (см)
(см)