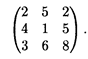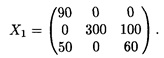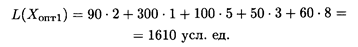|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Нахождение исходного опорного решения
Условия задачи и ее исходное опорное решение будем записывать в распределительную таблицу. Клетки, в которые поместим грузы, называются занятыми, им соответствуют базисные переменные опорного решения. Остальные клетки незанятые, или пустые, им соответствуют свободные переменные. В верхнем правом углу каждой клетки будем записывать тарифы. Существует несколько способов нахождения исходного опорного решения. Рассмотрим один из них — метод минимального тарифа (элемента). Согласно этому методу, грузы распределяются в первую очередь в те клетки, в которых находится минимальный тариф перевозок cij. Далее поставки распределяются в незанятые клетки с наименьшими тарифами с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей. Процесс распределения продолжают до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены. При распределении грузов может оказаться, что количество занятых клеток меньше, чем т + п - 1. В этом случае недостающее их число заполняется клетками с нулевыми поставками, такие клетки называют условно занятыми. Нулевые поставки помещают в незанятые клетки с учетом наименьшего тарифа таким образом, чтобы в каждых строке и столбце было не менее чем по одной занятой клетке. Рассмотрим нахождение исходного опорного решения транспортной задачи на конкретном примере.
23.3. Определение эффективного варианта доставки изделий к потребителю
На складах A1, А2, А3 имеются запасы продукции в количествах 90, 400, 110 т соответственно. Потребители В1, В2, B3 должны получить эту продукцию в количествах 140, 300, 160 т соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т продукции заданы матрицей (усл. ед.)
Проверим, является ли данная транспортная задача закрытой:
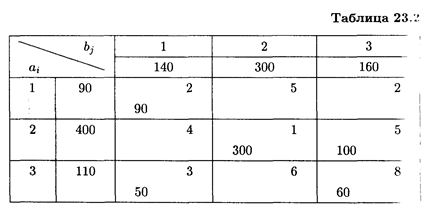
следовательно, данная транспортная задача закрытая. Найдем исходное опорное решение по методу минимального тарифа.
Число занятых клеток в табл. 23.2 равно т + п - 1 = 3 + 3 – 1 = 5, т.е. условие невырожденности выполнено. Получили исходное опорное решение, которое запишем в виде матрицы:
Стоимость перевозки при исходном опорном решении составляет
Поиск по сайту: |