 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основні поняття теорії ймовірностей ⇐ ПредыдущаяСтр 8 из 8
1 Яка подія називається достовірною, неможливою, випадковою? 2 Які події називаються несумісними, єдиноможливими, рівномож-ливими? 3 Що називається ймовіpністю події А? 4 Сформулюйте властивості ймовірності. 5 Що називається відносною частотою події А? 6 Дайте поняття статистичної ймовірності?
Основні теореми теорії імовірностей 1 Що називається сумою двох або декількох подій? 2 Сформулюйте і доведіть теорему додавання несумісних подій, її наслідок. 3 Що називається повною групою подій? 4 Сформулюйте теорему про повну групу подій. 5 Які події називаються протилежними? 6 Сформулюйте теорему про протилежні події та зауваження до неї. 7 Які події називаються незалежними, попарно незалежними, незалежними в сукупності? 8 Що називається добутком двох подій? 9 Сформулюйте і доведить теорему множення ймовірностей незалежних подій, її наслідок. 10 Довести теорему про ймовірність появи хоча б однієї події, її наслідок. 11 Які події називаються залежними? 12 Що називається умовною ймовірністю однієї події по відношенню до іншої? 13 Сформулюйте теорему множення залежних подій, її наслідок. 14 Які події називають сумісними? 15 Сформулюйте і доведіть теорему додавання ймовірностей несумісних подій та зауваження до неї. 16 Сформулюйте і доведіть теорему про повну ймовірність. 17 Вивести формулу Бейеса.
Повторні випробування 1 Які випробування називають незалежними? 2 Вивести формулу Бернуллі. 3 Сформулювати локальну теорему Лапласа. 4 Сформулювати інтегральну теорему Лапласа. 5 Вивести формулу для відхилення відносної частоти від сталої ймовірності в незалежних випробуваннях. 6 Вивести формулу Пуассона. 7 У яких випадках застосовуються формули Бернуллі, Лапласа, Пуассона. Дискретнівипадкові величини 1 Яку величину називають випадковою? 2 Дайте означення дискретної і неперервної випадкових величин. 3 Що називається законом розподілу дискретної випадкової величини? 4 Яким чином можна задати закон розподілу? 5 Що називається біноміальним розподілом? 6 Запишіть біноміальний закон розподілу, його числові характеристики.
Числові характеристики дискретних випадковиї величин 1 Що називається математичним сподіванням? Формула для обчислення математичного сподівання. 2 Імовірнісний зміст математичного сподівання. 3 Властивості математичного сподівання. 4 Математичне сподівання біноміального розподілу. 5 Що називається дисперсією дискретної випадкової величини? 6 Відхилення випадкової величини від її математичного сподівання, його властивість. 7 Формула для обчислення дисперсії. 8 Властивості дисперсії. 9 Дисперсія біноміального розподілу. 10 Середнє квадратичне відхилення, його властивість.
Інтегральна функція розподілу ймовірностей випадкової величини 1 Означення інтегральної функції розподілу. 2 Сформулюйте властивості інтегральної функції розподілу, що уявляє собою її графік.
Диференціальна функція розподілу ймовірностей неперервної випадкової величини 1 Означення диференціальної функції розподілу. 2 Імовірність попадання неперервної випадкової величини в заданий інтервал. 3 Знаходження інтегральної функції розподілу за відомою диферен-ціальною функцією. 4 Властивості диференціальної функції.
Закони розподілу та числові характеристики неперервних Випадкових величин 1 Дайте визначення закону рівномірного розподілу. 2 Що називається диференціальною функцією рівномірного розподілу. 3 Який має вигляд інтегральна функція рівномірного розподілу. 4 Числові характеристики рівномірного розподілу. 5 Дайте визначення нормального розподілу, нормальна крива. 6 Імовірність попадання в заданий інтервал нормальної випадкової величини. 7 Обчислення ймовірності заданого відхилення. 8 Сформулюйте правило трьох сигм.
Закон великих чисел
1 Довести нерівність Чебишева, сформулювати його значення. 2 Довести теорему Чебишева, її сутність і значення для практики. 3 Довести теорему Бернуллі. 4 Поняття збіжності за ймовірністю.
ДОДАТОК А Таблиця значень функції Гауса
Значення функції Лапласа
СПИСОК ЛІТЕРАТУРИ 1 Гмурман В. Е. Теория вероятностей и математическая статистика – М.: Высш. шк., 1977. 2 Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике – М.: Высш. шк., 1977. 3 Маркович Э.С. Курс высшей математики с элементами теории вероятностей и математической статистики. – М.: Высш.шк., 1976. 4 Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах – Т.3. – М.: Высш. шк., 1978. 5 Кремер Н.Ш. Теория вероятностей и математическая статистика – М.: ЮНИТИ, 2010.
ЗМІСТ
Навчальне видання
Методичні вказівки до виконання завдань модуля „випадкові події та випадкові величини” з курсу „Вища математика” для бакалаврів напрямів підготовки 6.040106; 6.050202; 6.050502; 6.060101; 6.060103
Укладачі: Аршава Олена Олександрівна Ізмайлова Світлана Георгіївна Щелкунова Любов Іванівна
Відповідальний за випуск О.О. Аршава
Редактор Л.І. Христенко
План 2009р., поз.78 Підп. до друку Формат 60х84 1/16. Надруковано на ризографі. Умов. друк. арк. 3.6 Тираж 100 прим. Обл.-вид. арк. 3.8. Папір друк. №2. Зам. № 1597 Безкоштовно. __________________________________________________________________ ХДТУБА, Україна, 61002, Харків, вул. Сумська, 40 __________________________________________________________________
Підготовлено та надруковано РВВ Харківського державного технічного університету будівництва та архітектури
Поиск по сайту: |
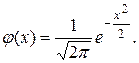
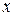
 ДОДАТОК Б
ДОДАТОК Б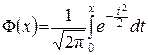 .
.