 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЗРАЗОК ВИКОНАННЯ ПІДСУМКОВОГО ЗАВДАННЯ
В урні знаходяться 15 червоних, 10 блакитних і 5 зелених куль. Навмання дістають 6 куль. Знайти ймовірність того, що витягнули 1 зелену, 2 блакитних, 3 червоних кулі (подія А). Розв’язання.В урні всього 30 куль. При даному випробуванні число всіх рівноможливих елементарних вихідів буде
4.1.2 Два автомати виготовляють однакові детали, які надходять на загальний конвеєр. Продуктивність першого автомата вдвічі більше другого. Перший автомат виготовляє 70% деталей відмінної якості, другий – 85%. Навмання взта з конвеєра деталь виявилась відмінної якості. Знайти ймовірність того, що ця деталь виготовлена першим автоматом. Розв’язання.Позначимо: подія А – деталь відмінної якості. Можна зробити два припущення: В1 – деталь виготовлена першим автоматом, причому за умовою задачі, перший автомат виготовляє вдвічі більше деталей, ніж другий, тому Умовна ймовірність того, що деталь відмінної якості виготовлена першим автоматом
Шукана ймовірність того, що взята деталь відмінної якості, виготовлена першим автоматом, за формулою Бейєса дорівнює:
Для нормальної роботи автобази на лінії повинні бути не менше 8 машин, а їх всього 10. Імовірність невиходу на лінію кожної автомашини дорівнює 0,1. Знайти ймовірність нормальної роботи автобази на найближчий день. Розв’язання.Автобаза буде працювати нормально (подія D), якщо на лінію вийдуть або 8 (подія А), або 9 (подія В), або 10 (подія С) автомашин. За теоремою додавання ймовірностей Р(D) = Р(А) + Р(В) + Р(С) = Р10(8) + Р10(9) + Р10(10). Кожний доданок знайдемо за формулою Бернуллі. Оскільки ймовірність невиходу автомашини на лінію дорівнює 0,1, то ймовірність виходу автомашини на лінію буде рівна 0,9, оскільки р=0,9, q=0,1. Із умови задачі n = 10, k = 8, 9, 10. Отже,
Імовірність появи події в кожному з 900 незалежних випробувань дорівнює 0,5. Знайти ймовірність того, що відносна частота появи події відхилиться від її ймовірності за абсолютною величиною не більше , ніж на 0,02. Розв’язання.За умовою задачі n = 900, р = 0,5, q = 0,5,
Скористаємося формулою
Маємо
Із доданка Б знаходимо
4.2.1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х прийме значення х1 дорівнює 0,45. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,1 і дисперсія D(Х) = 0,99. Розв`язання. Сума ймовірностей усіх можливих значень дискретної випадкової величини дорівнює 1, тому ймовірність того, що Х прийме значення х2, дорівнює 1 – 0,45 = 0,55. Запишемо закон розподілу Х: Х х1 х2 Р 0,45 0,55 Для знаходження х1 і х2 треба скласти два рівняння, які зв`язують ці числа. З цією метою виражаємо відомі М(Х) і D(Х) через х1 і х2. Знайдемо М(Х):М(Х) = 0,45х1 + 0,55х2. За умовою М(Х) = 3,1, отже, 0,45х1 + 0,55х2 = 3,1. Одне рівняння, яке звязує х1 і х2 отримали. Для того, щоб отримати друге рівняння, виразимо відому дисперсію через х1 і х2. Напишемо закон розподілу Х2: Х2 Р 0,45 0,55 Знайдемо дисперсію: D(X) = М(Х2) – М2(Х ) =
Помноживши обидві частини кожного рівняння системи на 20, отримаємо
Із першого рівняння знайдемо х1 і підставимо у друге рівняння:
Після перетворень розв`язуємо квадратне рівняння:
За умовою задачі х1 < х2, тому задачі задовольняє перший розвязок: х1 = 2, х2 = 4. Підставимо ці значення в закон розподілу: Х 2 4 Р 0,45 0,55. 4.2.2 Випадкова величина Х розподілена нормально з математичним сподіванням а=20 і середнім квадратичним відхиленням s =3. Знайти інтервал, у який з імовірностю 0,9973 попаде величина Х в результаті випробування. Розв`язання.Якщо ймовірність відхилення випадкової величини Х від свого математичного сподівання а дорівнює 0,9973, то відхилення менше потрійного середнього квадратичного відхилення. Тому інтервал, в який попаде ця величина, визначається нерівністю:
20-3•3 < X < 20+3•3. Отже, шуканий інтервал дорівнює (11, 29), або 11 < X < 29.
4.2.3 Імовірність появи події А в кожному випробуванні дорівнює 0,55. Застосовуючи нерівність Чебишева, оцінити ймовірність того, що число Х появи події А буде заключено в межах від 40 до 70, якщо буде проведено 100 незалежних випробувань. Розв`язання. Знайдемо математичне сподівання і дисперсію дискретної випадкової величини Х – числа появи події в 100 незалежних випробуваннях: M(X) = 100•0,55 = 55; D(X) = npq = 100•0,55•0,45 = 24,75. Mаксимальнa різниця між заданим числом появи події і математичним сподіванням М(Х) = 55:
Скористаємося нерівністю Чебишева:
Підставляючи M(X) = 55, D(X) = 24,75,
Поиск по сайту: |
 . Підрахуємо число елементарних виходів, які сприяють появі події А. Одну зелену кулю можна вибрати з 5
. Підрахуємо число елементарних виходів, які сприяють появі події А. Одну зелену кулю можна вибрати з 5  способами, 2 блакитних кулі з 10 можна вибрати
способами, 2 блакитних кулі з 10 можна вибрати  способами, 3 червоних з 15
способами, 3 червоних з 15  – способами. Отже ( в силу правила добутку в комбінаториці), число виходів, які сприяють події А, буде
– способами. Отже ( в силу правила добутку в комбінаториці), число виходів, які сприяють події А, буде  Шукану ймовірність знаходимо за формулою
Шукану ймовірність знаходимо за формулою
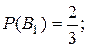 B2 – деталь виготовлена другим автоматом, причому
B2 – деталь виготовлена другим автоматом, причому 
 Для другого автомату ця ймовірність дорівнює
Для другого автомату ця ймовірність дорівнює  Імовірність того, що взята навмання деталь виявиться відмінної якості, обчислюється за формулою повної ймовірності:
Імовірність того, що взята навмання деталь виявиться відмінної якості, обчислюється за формулою повної ймовірності: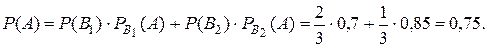

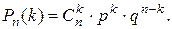
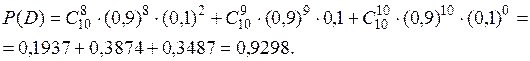
 = 0,02. Треба знайти ймовірність
= 0,02. Треба знайти ймовірність


 Отже, шукана ймовірність
Отже, шукана ймовірність
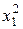

 Підставляючи D(X) = 0,99, після елементарних перетворень отримаємо
Підставляючи D(X) = 0,99, після елементарних перетворень отримаємо 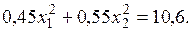 Таким чином, отримали систему двох рівнянь з двома невідомими:
Таким чином, отримали систему двох рівнянь з двома невідомими:









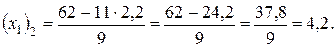
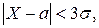
 або
або 


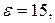 отримаємо
отримаємо