 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Неперервні випадкові величини
Дана щільність f(x) розподілу випадкової величини Х. Знайти: 1 Коефіцієнт с. 2 Інтегральну функцію розподілу F(x). 3 Побудувати графіки функцій f(x) і F(x). 4 Числові характеристики M(X); D(X); s(X). Варіант 1 Варіант 2
Варіант 3 Варіант 4
Варіант 5 Варіант 6
Варіант 7 Варіант 8
Варіант 9 Варіант 10
Варіант 11 Варіант 12
Варіант 13 Варіант 14 Варіант 15 Варіант 16
Варіант 17 Варіант 18
Варіант 19 Варіант 20
Варіант 21 Варіант 22
Варіант 23 Варіант 24
Варіант 25 Варіант 26
Варіант 27 Варіант 28
Варіант 29 Варіант 30
Рівномірний та нормальний розподіли випадкових величин
1 Дана щільність f(x) рівномірно розподіленої випадкової величини Х (таблиця 1).
Знайти: а) інтегральну функцію розподілу F(x); б) побудувати графіки функцій F(x), f(x); в) числові характеристики рівномірного розподілу M(X), D(X), s(X). Таблиця 1
2 Неперервна випадкова величина має нормальний розподіл. Її математичне сподівання дорівнює а, середнє квадратичне відхилення s (таблиця 2). Знайти: а) імовірність попадання випадкової величини Х в інтервал (a; b); б) імовірність абсолютної величини відхилення випадкової величини Х від її математичного сподівання; в) імовірність того, що
Таблиця 2
ВАРІАНТИ ПІДСУМКОВОГО ЗАВДАННЯ Розв’язати задачі, використовуючи теорію випадкових подій. Варіант 1 1 У конверті серед 100 фотографій знаходиться 1, яку розшукують. Із конверта навмання беруть 10 фотографій. Знайти ймовірність того, що серед них знаходиться розшукувана. 2 Перша коробка містить 30 радіоламп, з яких 12 стандартних, друга – 20 ламп, з яких 15 стандартних. Із другої коробки навмання взята лампа і перекладена в першу. Знайти ймовірність того, що лампа взята навмання з першої коробки буде стандартна. 3 Знайти ймовірність того, що подія А настає 60 разів у 350 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,65. 4 Імовірність появи події в кожному із 200 випробувань дорівнює 0,7. Знайти ймовірність того, що ця подія з’явиться від 60 до 85 разів. Варіант 2 1 У партії з 15 деталей 8 – стандартних. Знайти ймовірність того, що серед 6 взятих навмання деталей 4 будуть стандартні. 2 У групі спортсменів: 25 лижників, 10 велосипедистів, 15 бігунів. Імовірність виконати кваліфікаційну норму така: для лижника 0,9, для велосипедиста 0,85, для бігуна 0,7. Знайти ймовірність того, що спортсмен вибраний навмання виконає норму. 3 Знайти ймовірність того, що подія А настає 80 разів у 500 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,6. 4 Імовірність появи події в кожному з 800 незалежних випробувань дорівнює 0,9. Знайти ймовірність того, що відносна частота появи події відхилиться від її ймовірності за абсолютною величиною не більше, ніж на 0,03. Варіант 3 1 У першості з футболу брали участь 18 команд, з яких 5 лідирує. Команди розподіляють на 2 групи по 9 команд. Яка ймовірність попадання всіх команд, що лідирує, в одну групу. 2 Складальник отримав 3 коробки деталей, вироблених на заводі №1 і 4 коробки деталей завода №2. Імовірність того, що деталь завода №1 стандартна дорівнює 0,7, а завода №2 – 0,9. Складальник навмання взяв деталь із навмання вибраної коробки. Знайти ймовірність того, що взята стандартна деталь. 3 Знайти ймовірність того, що подія А настає 70 разів у 400 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,55. 4 Завод відправив на базу 1500 якісних виробів. Імовірність пошкодження кожного виробу в дорозі дорівнює 0,0001. Знайти ймовірність того, що в дорозі буде пошкоджено 3 вироби. Варіант 4 1 Навмання взятий телефонний номер складається з 5 цифр. Яка ймовірність того, що в номері всі цифри різні. 2 Два автомати виготовляють однакові деталі. Продуктивність першого автомата вдвічі більше другого. Виготовлення деталей відмінної якості для автоматів відповідно дорівнює 0,7; 0,8. Взята навмання деталь виявилась відмінної якості. Знайти ймовірність того, що ця деталь зроблена першим автоматом. 3 Знайти ймовірність того, що подія А настає 80 разів у 300 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,7. 4 Імовірність появи події в кожному із 400 випробувань дорівнює 0,8. Знайти ймовірність того, що ця подія з’явиться від 65 до 75 разів. Варіант 5 1 На полиці 25 підручників, з яких 5 з теорії імовірностей. Студент навмання бере 2 підручники. Знайти ймовірність того, що вони з теорії імовірностей. 2 У телевізійному ательє 4 кінескопи. Імовірності того, що кінескоп витримає гарантійний строк, відповідно дорівнюють: 0,6; 0,7; 0,8; 0,9. Знайти ймовірність того, що взятий навмання кінескоп витримає гарантійний строк. 3 Знайти ймовірність того, що подія А настає 75 разів у 600 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,75. 4 Імовірність появи події в кожному з 750 незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що відносна частота появи події відхилиться від її ймовірності за абсолютною величиною не більше, ніж на 0,02. Варіант 6 1 Тризначне число утворене неповторними цифрами із цифр 1, 2, 3, 4, 5. Знайти ймовірність того, що це число парне. 2 Знайти ймовірність того, що навмання взяте двозначне число буде кратне 3 або 7, або 3 і 7. 3 У партії з 24 виробів 6 – браковані. Яка ймовірність того, що серед взятих навмання 4 виробів 2 – будуть бракованими. 4 Знайти ймовірність того, що подія А наступе 65 разів у 550 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,6. Варіант 7. 1 Задумано двозначне число, цифри якого різні. Знайти ймовірність того, що задуманим числом виявиться випадково назване двозначне число. 2 Деякий виріб випускається двома заводами, причому другий завод випускає виробів в 4 рази більше першого. Імовірність брака для кожного завода відповідно дорівнює 0,02; 0,01. Знайти ймовірність того, що придбаний бракованій виріб виготовлено на другому заводі. 3 У партії з 30 виробів 6 – бракованих. Яка ймовірність того, що серед взятих навмання 5 виробів 2 будуть бракованими. 4 Знайти ймовірність того, що подія А настає 85 разів у 750 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,65. Варіант 8 1 При перевезенні ящика, в якому знаходились 21 стандартний і 10 нестандартних виробів, загубили 1 виріб, причому невідомо який. Навмання взятий з ящика виріб виявився стандартним. Знайти ймовірність того, що загубили стандартний виріб.. 2 На виробництві виготовляють вироби на трьох поточних лініях. Кількість виробів кожної лінії відповідно складає 35 %, 20 %, 45%. Відсоток стандартних виробів для кожної лінії відповідно дорівнює 0,96; 0,97; 0,98. Знайти ймовірність того, що взятий навмання стандартний виріб виготовлен на 3 лінії. 3 Знайти ймовірність того, що подія А настає 90 разів у 1600 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,7. 4 Імовірність появи події в кожному з 1000 незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що відносна частота появи події відхилиться від її ймовірності за абсолютною величиною не більше, ніж на 0,03. Варіант 9 1 У ящику 100 деталей, серед них 10 бракованих. Навмання беруть 4 деталі. Знайти ймовірність того, що серед взятих деталей будуть 3 стандартні. 2 У цеху три типи автоматичних верстатів. Продуктивність їх однакова, а якість різна. Відмінна якість верстатів відповідно дорівнює 0,8; 0,9; 0,85. Кількість верстаті типів відповідна 5, 3, 2. Взятий навмання виріб виявився відмінної якості. Знайти ймовірність того, що цей виріб належить верстату першого типу. 3 У партії з 30 виробів 6 – браковані. Яка ймовірність того, що серед взятих навмання 10 виробів 4 – будуть бракованими. 4.Знайти ймовірність того, що подія А настає 65 разів у 800 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,7. Варіант 10 1 Гральну кістку кидають двічі. Знайти ймовірність того, що обидва рази з'явиться однакове число очок. 2 На складання потрапляють деталі з трьох автоматів. Брак відповідно складає 0,2 % , 0,3 % , 0,4 %. Знайти ймовірність попадання на складання бракованої детали, якщо з першого автомата поступило 1600, з другого – 2000, з третього – 2400 деталей. 3 У партії з 20 виробів 5 – браковані. Яка ймовірність того, що серед взятих навмання 4 виробів 3 будуть бракованими. 4 Знайти ймовірність того, що подія А настає 60 разів у 900 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,8. Варіант 11 1 У групі 25 студентів, серед яких 6 відмінників. Навмання відбирають 10 студентів. Знайти ймовірність того, що серед них будуть 5 відмінників. 2 На двох автоматичних верстатах виробляються однакові вироби. Продуктивність першого верстата вдвічі більше, ніж другого. Імовірність виготовлення вироба вищої якості відповідно дорівнює 0,75 і 0,9. Знайти ймовірність того, що взятий навманння виріб буде вищої якості. 3 У партії з 30 виробів 6 – браковані. Яка ймовірність того, що серед взятих навмання 4 виробів 3 будуть бракованими. 4 Знайти ймовірність того, що подія А настає 100 разів у 1900 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,7. Варіант 12 1 У коробці 10 однакових виробів, серед яких 7 пофарбованих. Навмання беруть 5 виробів. Знайти ймовірність того, що серед них 3 пофарбовані. 2 У групі 30 чоловік, з них 12 хлопців і 18 дівчат. Із хлопців до семінара підготувались 8 чоловік, а з дівчат – 12. Когось визвали і відповідь була дана. Знайти ймовірність того, що була визвана дівчина. 3 У партії з 20 виробів 4 – браковані. Яка ймовірність того, що серед взятих навмання 3 виробів 2 будуть бракованими. 4 Знайти ймовірність того, що подія А настає 75 разів у 600 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,7. Варіант 13 1 Збори, на яких присутні 25 чоловік, в тому числі 5 жінок, обирають делегацію з 3 чоловік. Знайти ймовірність того, що в делегацію увійдуть 2 жінки і 1 чоловік. 2 Три верстати працюють незалежно один від іншого. Імовірність безперебійної роботи протягом зміни для першого верстата дорівнює 0,6, для другого – 0,8, для третього – 0,7. Знайти ймовірність того, що протягом зміни тільки один верстат працює безперебійно. 3 У партії з 32 виробів 8 – браковані. Яка ймовірність того, що серед взятих навмання 5 виробів 2 будуть бракованими. 4 Знайти ймовірність того, що подія А настає 70 разів у 1000 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,8. Варіант 14 1 У лотереї 100 білетів, з яких 25 виграшних. Знайти ймовірність того, що кожний із двох отриманих білетів буде виграшним. 2 Студент знає 40 з 60 питань програми. Кожний екзаменаційний білет містить 3 питання. Знайти ймовірність того, що студент знає хоча б одне питання. 3 Знайти ймовірність того, що подія А настає 65 разів у 1000 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,7. 4 Імовірність появи події в кожному з 1000 незалежних випробувань дорівнює 0,8. Знайти імовірність того, що відносна частота появи події відхилиться від її ймовірності за абсолютною величиною не більше, ніж на 0,03. Варіант 15 1 На тепловій електростанції 15 змінних інженерів, з яких 4 жінки. В зміну зайнято 3 інженери. Знайти ймовірність того, що в навмання вибрану зміну попадуть 2 чоловіка. 2 В урні 6 білих, 4 чорних і 10 синіх кулі. Випробування полягає в тому, що навмання з урни беруть кулю, не повертаючи її в урну. Знайти ймовірність того, що при першому випробуванні з’явиться біла куля, при другому – чорна, при третьому – синя. 3 У партії з 25 виробів 5 – браковані. Яка ймовірність того, що серед взятих навмання 4 виробів 2 будуть бракованими. 4 Знайти ймовірність того, що подія А настає 70 разів у 900 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,85. Варіант 16 1 На п’яти картках написані літери А, З, І, Л, К. Після перемішування беруть по одній картці й кладуть послідовно рядом. Знайти ймовірність того, що буде отримано слово ЗАЛІК. 2 У піраміді 15 гвинтівок, 5 з яких обладнані оптичним прицілюванням. Імовірність того, що стрілець влучить у мішень з гвинтівки з прицілюванням дорівнює 0,95, без прицілювання – 0,77.Знайти ймовірність того, що в мішень буде влучено з навмання взятої гвинтівки. 3 Знайти ймовірність того, що подія А настає 90 разів у 1800 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,6. 4 Імовірність того, що будь-який із 3000 абонентів зателефонує на комутатор протягом години дорівнює 0,03. Знайти ймовірність того, що протягом години зателефонує 2 абоненти. Варіант 17 1 Збори, на яких присутні 25 чоловік, у тому числі 6 жінок, обирають делегацію з трьох чоловік. Знайти ймовірність того, що в делегацію увійдуть 1 жінка і 2 чоловіки. 2 На фабриці виготовляють вироби на трьох поточних лініях. Вироби з кожної лінії відповідно складають: 40 %, 35 %, 25 %. Стандартність виробів на кожній лінії відповідно дорівнює 97 %, 96 %, 94 %. Знайти ймовірність того, що навмання взятий виріб буде бракованим. 3 Знайти ймовірність того, що подія А настає 90 разів у 1500 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,7. 4 Імовірність появи події в кожному з 1800 випробувань дорівнює 0,6. Знайти ймовірність того, що ця подія з’явиться від 63 до 73 разів. Варіант 18 1 Кинуто дві гральні кістки. Знайти ймовірність того, що сума очок на них дорівнює 7, а добуток 12. 2 Ящик містить однакові вироби, де 30 % виготовлені першим автоматом, інші – другим. Брак продукції відповідно складає 3 %, 5 %. Знайти ймовірність того, що навмання взятий виріб буде бракованим. 3 Знайти ймовірність того, що подія А настає 65 разів у 800 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,75. 4 Імовірність того, що будь-який з 1500 абонентів зателефонує на комутатор протягом години дорівнює 0,03. Знайти ймовірність того, що протягом години зателефонує 2 абоненти. Варіант 19 1 У партії з 100 виробів 10 – бракованих. Знайти ймовірність того, що серед взятих 4 виробів 3 будуть не браковані. 2 На підприємстві працюють три поточні лінії.На кожній лінії виробляють відповідно виробів: 30 %, 25 %. 45 % . Стандартність виробу для кожної лінії відповідно дорівнює 95 %, 96 %, 97 %. Знайти ймовірність того, що навмання взятий виріб буде бракованим. 3 Знайти ймовірність того, що подія А настає 70 разів у 950 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,75. 4 Імовірність появи події в кожному з 1800 випробувань дорівнює 0,6. Знайти ймовірність того, що ця подія з’явиться від 55 до 65 разів. Варіант 20 1 На 100 картках написані числа від 1 до 100. Знайти ймовірність того, що випадково взята картка містить цифру 5. 2 На підприємстві працюють дві бригади робітників: перша – виготовляє 0,8 продукції з відсотком брака 4 %, друга – 0,2 продукції з відсотком брака 5 %. Знайти ймовірність того, що взятий навмання бракований виріб був виготовлений другою бригадою. 3 У партії з 15 виробів 6 – бракованих. Яка ймовірність того, що серед взятих навмання 4 виробів 2 будуть бракованими. 4 Знайти ймовірність того, що подія А настає 75 разів у 1000 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,7. Варіант 21 1 Кинуто дві гральні кістки. Знайти ймовірність того, що сума очок, які з’явилися на випавши гранях, дорівнює 6. 2 Ящик містить 15 виробів завода №1, серед яких 1 – бракований, 10 виробів заводу № 2, серед яких 2 – бракованих, 25 виробів заводу № 3, серед яких 3 – браковані. Навмання взятий виріб виявився бракованим. Знайти ймовірність того, що цей виріб заводу № 3. 3 Знайти ймовірність того, що подія А настає 80 разів у 1000 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,7. 4 Імовірність появи події в кожному з 1500 незалежних випробувань дорівнює 0,75. Знайти ймовірність того, що відносна частота появи події відхилиться від її ймовірності за абсолютною величиною не більше, ніж на 0,03. Варіант 22 1 На 30 однакових картках написані 30 двозначних чисел від 11 до 40. Картки ретельно перемішують. Знайти ймовірність того, що навмання витягнута картка буде з номером кратним 5. 2 У будзагоні 60 % першокурсників і 40 % студентів другого курсу. Серед першокурсників – 20 % дівчат, а серед другокурсників – 10%. Усі дівчата по черзі чергують на кухні. Знайти ймовірність того, що в навмання вибраний день на кухні чергуюють дівчата. 3 У партії з 35 виробів 7 – браковані. Яка ймовірність того, що серед взятих навмання 5 виробів 3 будуть бракованими. 4 Знайти ймовірність того, що подія А настає 75 разів у 950 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,65. Варіант 23 1 У студентській групі 28 чоловік, серед яких 20 студентів старше 22 років. При жеребкуванні розигрується 1 запрошувальний білет на вечір. Знайти ймовірність того, що білет виграє студент старше 22 років. 2 У обчислюваній лабораторії 4 клавішних автоматів і 6 напівавтоматів. Імовірність того, що під час виконання деякого розрахунку автомат не вийде із ладу дорівнює 0,9, для напівавтомата – 0,85. Наавмання вибирається машина. Знайти ймовірність того, що під час розрахунку вибрана машина не вийде із ладу. 3 Знайти ймовірність того, що подія А настає 82 рази в 1600 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,76. 4 Імовірність появи події в кожному з 1200 незалежних випробувань дорівнює 0,63. Знайти ймовірність того, що відносна частота появи події відхилиться від її ймовірності за абсолютною величиною не більше, ніж на 0,02. Варіант 24 1 Кинуто дві гральні кістки. Знайти імовірність того, що сума очок на них буде менше 8. 2 Чотири верстати виготовляють деталі. Брак відповідно до верстатів складає: 0,2%, 0,35%, 0,3%, 0,4%. Продуктивності верстатів відносяться як 5: 3: 2: 1. На збирання надійшла стандартна деталь. Знайти ймовірність того, що ця деталь зроблена на четвертому верстаті. 3 Знайти ймовірність того, що подія А настає 58 разів у 950 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,75. 4 Імовірність того, що будь-який з 1800 абонентів зателефонують на комутатор протягом години дорівнює 0,02. Знайти ймовірність того, що протягом годинизателефонують 3 абоненти. Варіант 25 1 В студентській групі 10 спортсменів, серед яких 7 юнаків і 3 дівчини. Трьох спортсменів обирають для участі в змаганнях. Знайти ймовірність того, що обраними будуть 3 юнаки. 2 Четверта частина виробів однієї з трьох партій – другосортна, інші вироби в усіх партіях – першосортні. Навмання взятий виріб із однієї партії виявився першосортним. Знайти ймовірність того, що виріб був взятий із партії, яка має другосортні вироби. 3 Знайти ймовірність того, що подія А настає 85 разів у 1950 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,85. 4 Імовірність появи події в кожному із 1780 випробувань дорівнює 0,86. Знайти ймовірність того, що ця подія з’явиться від 75 до 83 разів. Варіант 26 1 У коробці 10 однакових виробів, серед яких 7 – пофарбовані. Навмання беруть 5 виробів. Знайти ймовірність того, що серед взятих виробів 3 – пофарбованi. 2 У телевізійному ательє 5 кінескопів. Імовірності того, що кінескоп витримає гарантійний строк, відповідно дорівнюють: 0,7; 0,8; 0,9; 0,6; 0,65. Знайти ймовірність того, що взятий навмання кінескоп витримає гарантійний строк. 3 У партії з 40 виробів 8 – браковані. Яка ймовірність того, що серед взятих навмання 6 виробів 4 будуть бракованими. 4 Знайти ймовірність того, що подія А настає 95 разів у 1750 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,75. Варіант 27 1 Учасники жеребкування беруть із ящика жетони з номерами від 1 до 100. Знайти ймовірність того, що навмання взятий перший жетон не містить цифри 5. 2 Складальник отримав 3 коробки деталей, вироблених на заводі №1, і коробки деталей заводу №2. Імовірність того, що деталь заводу №1 стандартна дорівнює 0,7, а заводу №2 – 0,8. Складальник навмання взяв деталь із навмання вибраної коробки. Знайти ймовірність того, що взята стандартна деталь. 3 Знайти ймовірність того, що подія А настає 78 разів у 980 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,8. 4 Імовірність того, що будь-який з 1000 абонентів зателефонує на комутатор протягом години дорівнює 0,02. Знайти ймовірність того, що протягом години зателефонує 3 абоненти. Варіант 28 1 На 6 картках написані літери А, А, А, Н, Н, С. Картки ретельно перемішані, потім їх розкладають в ряд. Знайти ймовірність того, що отримали слово АНАНАС. 2 Прилад складається з двох вузлів. Імовірність відмовлення вузла відповідно дорівнює 0,02; 0,03. Під час випробування прилад вийшов з ладу. Знайти ймовірність того, що відмовив перший вузол. 3 У партії з 32 виробів 8 – браковані. Яка ймовірність того, що серед взятих навмання 5 виробів 3 будуть бракованими. кіл. 4 Імовірність появи події в кожному з 1850 випробувань дорівнює 0,85. Знайти ймовірність того, що ця подія з’явиться від 77 до 87 разів. Варіант 29 1 У середині круга з радіусом 20 см проведено два кола, які не перетинаються – одне з радіусом 5 см, друге – з радіусом 10 см. Знайти ймовірність того, що точка, поставлена навмання у середині великого кола, буде знаходитися у середині одного із малих кіл. 2 Два автомати виробляють деталі, які надходять на загальний конвеєр. Імовірність отримати браковану деталь від автомата відповідно дорівнює 0,03; 0,05. Продуктивність першого автомата вдвічі менша продуктивності другого. Навмання взята з конвеєра деталь виявилась стандартною. Знайти імовірність того, що вона виготовлена другим автоматом. 3 Імовірність появи події в кожному з 1400 незалежних випробувань дорівнює 0,63. Знайти ймовірність того, що відносна частота появи події відхилиться від її ймовірності за абсолютною величиною не більше, ніж на 0,02. 4 У партії з 24 виробів 4 – браковані. Яка ймовірність того, що серед взятих навмання 5 виробів 2 будуть бракованими. Варіант 30 1 Із п’яти букв розрізної азбуки складаємо слово “книга”. Дитина, яка не вміє читати, розсипала ці букви і потім зібрала їх в довільному порядку. Знайти ймовірність того, що вона знову отримає слово “книга”. 2 Два стрільці стріляють по мішені 1 раз. Імовірності влучення в мішень під час одного пострілу дорівнюють для першого стрільця 0,65, для другого – 0,75. Знайти ймовірність того, що в мішень буде влучено тільки одним стрільцем. 3 Знайти ймовірність того, що подія А настає 70 разів у 400 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,8. 4 Завод відправив на базу 1000 якісних виробів. Імовірність пошкодження кожного виробу в дорозі дорівнює 0,0002. Знайти ймовірність того, що в дорозі буде пошкоджено 3 вироби. 3.2 Розв’язатити задачі, використовуючи теорію випадкових величин Варіант 1 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,1. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,9, а дисперсія D(Х) = 0,09. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=12 і середнім квадратичним відхиленням s = 4. Знайти інтервал, у який із імовірностю 0,9973 попаде Х в результаті випробування. 3 Оцінити ймовірність того, що число осіб, які мають вищу освіту, в групі з 800 чоловік, відрізняється від свого математичного сподівання, рівного 200, менше, ніж на 40. Варіант 2 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,3. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,7, а дисперсія D(Х) = 0,21. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=10 і середнім квадратичним відхиленням s = 6. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Скільки повинно бути проведено незалежних вимірювань деякої величини, щоб з імовірністю, не меншою ніж 0,95, можна було стверджувати, що середнє арифметичне результатів вимірювання відрізняється від істинного значення за абсолютною величиною менше, ніж на 2, якщо середнє квадратичне відхилення кожної величини менше 10? Варіант 3 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,5. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,5, а дисперсія D(Х) = 0,25. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=8 і середнім квадратичним відхиленням s = 3. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Імовірність виготовлення нестандартної радіолампи дорівнює 0,02. Яку кількість радіоламп треба відібрати, щоб з імовірністю більшою 0,8, можна було стверджувати, що частина серед них нестандартних радіоламп буде відрізняться від імовірності виготовлення нестандартної лампи за абсолютною величиною не більше, ніж на 0,005? Варіант 4 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,7. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,3, а дисперсія D(Х) = 0,21. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=10 і середнім квадратичним відхиленням s = 8. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 При штампуванні 70 % виробів є першосортними. Скільки треба взяти виробів, щоб з імовірністю, яка не превищує 0,9973, можна було б стверджувати, що частина першосортних серед них буде відрізняться за абсолютною величиною від імовірності р = 0,7 не більше, ніж на 0,05? Варіант 5 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,9. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,1, а дисперсія D(Х) = 0,09. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=9 і середнім квадратичним відхиленням s = 4. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Середня вага картоплини дорівнює 120 г. Яка ймовірність того, що навмання взята картоплина має вагу не більше 360 г? Варіант 6 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,9. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 2,2, а дисперсія D(Х) = 0,36. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=9 і середнім квадратичним відхиленням s = 6. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Середнє число молодих спеціалістів, яких щорічно направляють до аспірантури, складає 200 чоловік. Оцінити ймовірність того, що в цьому році до аспірантури буде направлено не більше 220 молодих спеціалістів. Варіант 7 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,8. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,2, а дисперсія D(Х) = 0,16. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=7 і середнім квадратичним відхиленням s = 4. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Імовірність появи події А в кожному випробуванні р=0,5. Використовуючи нерівність Чебишева, оцінити ймовірність того, що число появи події А включено в межах від 40 до 60, якщо буде проведено 100 випробувань. Варіант 8 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,6. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,4, а дисперсія D(Х) = 0,24. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=10 і середнім квадратичним відхиленням s = 3. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Імовірність виготовлення нестандартного виробу в деяких технологічних умовах дорівнює 0,1. Оцінити ймовірність того, що число нестандартних виробів серед 10000 буде включено в межах від 950 до 1030 включно. Варіант 9 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,4. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,6, а дисперсія D(Х) = 0,24. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=8 і середнім квадратичним відхиленням s = 2. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Імовірність сходження насіння деякої культури дорівнює 0,75. Оцінити ймовірність того, що з посіяних 1000 зерен насіння, зійде від 700 до 800 зерен включно. Варіант 10 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,2. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,8, а дисперсія D(Х) = 0,16. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=11 і середнім квадратичним відхиленням s = 4. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Електростанція обслуговує мережу в 20000 ламп, імовірність включення кожної з яких в зимовий період дорівнює 0,8. Яка ймовірність того, що число ламп, включених в мережу зимовим вечором, відрізняється від свого математичного сподівання за абсолютною величиною не більше, ніж на 300. Варіант 11 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,2. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 2,6, а дисперсія D(Х) = 0,64. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=9 і середнім квадратичним відхиленням s = 2. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Імовірність появи події А в кожному з 1500 випробувань дорівнює 0,4. Використовуючи нерівність Чебишева, оцінити ймовірність того, що відхилення числа появи цієї події від математичного сподівання буде більше 25. Варіант 12 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,9. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,2, а дисперсія D(Х) = 0,36. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=14 і середнім квадратичним відхиленням s = 8. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Число телевізорів вищої якості складає в середньому 75 % від їх загального випуска. Оцінити за допомогою нерівності Чебишева ймовірність того, що серед 2000 телевізорів число телевізорів вищої якості буде від 1790 до 1920 включно. Варіант 13 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,8. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 1,8, а дисперсія D(Х) = 2,56. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=12 і середнім квадратичним відхиленням s = 6. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Скільки треба перевірити виробів, щоб з імовірністю, не меншою ніж 0,98, можна було б чекати, що абсолютна величина відхилення частоти придатних виробів від імовірності вироба бути придатним, рівній 0,95, не перевищує 0,01. Варіант 14 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,8. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 1,2, а дисперсія D(Х) = 0,16. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=14 і середнім квадратичним відхиленням s = 5. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Імовірність того, що випущений годинник має точність ходу в межах стандарта, дорівнює 0,97. Оцінити ймовірність того, що серед 1000 годинників частина годинників з точністю ходу в межах норми відхилиться за абсолютною величиною від імовірності 0,97 не більше, ніж на 0,02. Варіант 15 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,7. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 2,2, а дисперсія D(Х) = 3,36. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=15 і середнім квадратичним відхиленням s = 4. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 У процесі штампування платівок з пластмаси за даними ВТК брак складає 3%. Знайти ймовірність того, що під час перегляду партії в 2000 платівок виявиться відхилення від установленого процента браку менше, ніж на 1 %.
Варіант 16 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,3. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,7, а дисперсія D(Х) = 0,21. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=14 і середнім квадратичним відхиленням s = 7. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Дисперсія кожної з попарно незалежних випадкових величин не перевищує 6. Визначити, скільки таких випадкових величин треба взяти, щоб з імовірністю, не менше 0,99, можна було б стверджувати, що Варіант 17 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,6. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,2, а дисперсія D(Х) = 0,16. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=14 і середнім квадратичним відхиленням s = 8. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Дисперсія кожної з попарно незалежних 15000 випадкових величин не перевищує 8. Оцінити ймовірність того, що відхилення середнього арифметичного цих величин від математичного сподівання їх середньої не перевищує 0,3. Варіант 18 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,4. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = =2,8, а дисперсія D(Х) = 2,16. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=14 і середнім квадратичним відхиленням s = 9. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Відомо, що дисперсія кожної з незалежних випадкових величин не превищує 4. Визначити число таких величин, при якому ймовірність відхилення середнього арифметичного випадкових величин від середнього арифметичного їх математичних сподівань не більше, ніж на 0,25, перевищує 0,99. Варіант 19 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,5. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 4,5, а дисперсія D(Х) = 0,25. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=15 і середнім квадратичним відхиленням s = 5. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Довжина виробляємих стрижнів представляє випадкову величину з математичним сподіванням рівним 90 см і дисперсією – 0,0225. Оцінити ймовірність того, що відхилення довжини виробленого стержня від математичного сподівання за абсолютною величиною не перевищує 0,4 см. Варіант 20 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,5. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,0, а дисперсія D(Х) = 1,0. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=14 і середнім квадратичним відхиленням s = 10. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Середнє значення довжини виробу 50 см, а дисперсія 0,1. Використовуючи нерівність Чебишева, оцінити ймовірність того, що навмання взятий виріб буде за довжиною не менше 49,5 і не більше 50,5 см. Варіант 21 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,4. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 2,2, а дисперсія D(Х) = 0,96. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=14 і середнім квадратичним відхиленням s = 4. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Скільки повинно бути проведено незалежних вимірювань деякої величини, щоб з імовірністю, не меншою, ніж 0,98 можна було стверджувати, що середнє арифметичне результатів вимірювання відрізняється від істинного значення за абсолютною величині менше, ніж на 0,01, якщо дисперсія кожного результата вимірювання не перевищує 1? Варіант 22 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,6. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 2,4, а дисперсія D(Х) = 0,24. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=16 і середнім квадратичним відхиленням s = 9. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Дискретна випадкова величина задана законом розподілу Х 0,3 0,6 Р 0,2 0,8 Використовуючи нерівність Чебишева, оцінити ймовірність того, що Варіант 23 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,3. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 3,4, а дисперсія D(Х) = 0,84. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=16 і середнім квадратичним відхиленням s = 5. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Нехай в результаті 100 незалежних спроб знайдені значення випадкової величини Х: х1, х2, ...., х100. Відомі: математичне сподівання М(Х) = 10 і дисперсія D(Х) = 1. Оцінити ймовірність того, що абсолютна величина різниці між середнім арифметичним Варіант 24 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,7. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 1,3, а дисперсія D(Х) = 0,21. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=15 і середнім квадратичним відхиленням s = 8. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Імовірність появи події в кожному випробуванні дорівнює 0,3. Застосувавши нерівність Чебишева, знайти число випробувань, необхідних для того, щоб імовірність відхилення частоти події від її ймовірності була б за абсолютною величиною більше 0,99. Варіант 25 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,1. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 1,9, а дисперсія D(Х) = 0,09. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=15 і середнім квадратичним відхиленням s = 7. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Зріст дорослих чоловіків в їх сукупності, що розглядається, є нормально розподіленою величиною з математичним сподіванням а = 170 см і дисперсією D = 36 см. Визначити ймовірність того, що хоча б один навмання вибраний дорослий чоловік буде мати зріст від 165 см до 175 см. Варіант 26 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,7. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 1,6, а дисперсія D(Х) = 0,84. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=18 і середнім квадратичним відхиленням s = 7. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Діаметр виготовлених поршнів є випадковою величиною, розподіленою за нормальним законом, з математичним сподіванням а = 4 і дисперсією D(Х) = =9*10-6 . Поршні з діаметром 3,994 і 4,006 є браком. Який при цих умовах очікується процент браку? Варіант 27 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,5. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 2,5, а дисперсія D(Х) = 0,25. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=14 і середнім квадратичним відхиленням s = 2. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Відхилення довжини виготовлених виробів від стандарта є випадковою величиною, розподіленою за нормальним законом. Якщо стандартна довжина дорівнює 40 см і середнє квадратичне відхилення s = 0,4 см, тоді яку точність довжини виробу можна гарантувати з імовірністю 0,8? Варіант 28 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,8. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 1,4, а дисперсія D(Х) = 0,64. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=18 і середнім квадратичним відхиленням s = 10. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 У читальному залі установлено 200 настільних ламп, які включаються і виключаються незалежно одна від іншої. Для кожної лампи ймовірність бути включеною дорівнює 0,8. Знайти ймовірність того, що абсолютна величина різниці між числом включених ламп і математичним сподіванням цього числа буде більше 10. Варіант 29 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,9. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 2,2, а дисперсія D(Х) = 0,36. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=15 і середнім квадратичним відхиленням s = 7. Знайти інтервал, уякий з імовірностю 0,9973 попаде Х в результаті випробування. 3 Математичне сподівання швидкості повітря на даній висоті дорівнює 25 км /год. Середнє квадратичне відхилення дорівнює 4,5 км/год. Які швидкості повітря на цій висоті можна очикувати з імовірністю, не меншою за 0,9?
Варіант 30 1 Дискретна випадкова величина Х має тільки два можливих значення: х1 і х2, причому х1 < х2. Імовірність того, що Х приймає значення х1 дорівнює 0,9. Знайти закон розподілу величини Х, якщо математичне сподівання М(Х) = 1,3, а дисперсія D(Х) = 0,81. 2 Випадкова величина Х розподілена нормально з математичним сподіванням а=18 і середнім квадратичним відхиленням s = 9. Знайти інтервал, у який з імовірностю 0,9973 попаде Х в результаті випробування. 3 Електростанція обслуговує мережу в 18000 ламп, імовірність включення кожної дорівнює 0,9. Чому дорівнює ймовірність того, що число включених ламп в мережу відрізняється від свого математичного сподівання за абсолютною величиною не більше, ніж на 200 ламп?
Поиск по сайту: |


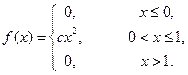
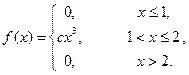




















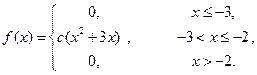


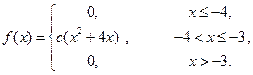





 , якщо звісна дисперсія D(X).
, якщо звісна дисперсія D(X). не перевищує 0,25.
не перевищує 0,25.
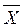 значень, що спостерігаються, випадкової величини і математичним сподіванням менше 0,5.
значень, що спостерігаються, випадкової величини і математичним сподіванням менше 0,5.