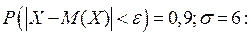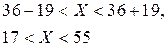|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ВАРІАНТ МОДУЛЬНОГО КОНТРОЛЮ ТА ПРИКЛАД ЙОГО ВИКОНАННЯ
Варіант МК
Тестова частина 1 Яка подія називається достовірною? А Подія, яка може наступати, або не наступати. Б Подія, яка обов’язково наступає при виконанні визначеної сукупності умов. В Подія, яка не наступає при виконанні визначеної сукупності умов. Г Подія, появу якої не можна спрогнозувати.
2 Подія А – випадкова. Які значення приймає її ймовірність Р(А)? А Р(А) = 0. Б Р(А)>1. В 0 Г Р(А) = 1.
3 Події А і В – сумісні, їх імовірності: Р(А), Р(В). Чому дорівнює ймовірність появи хоча б однієї події Р(А+В)? А Р(А+В) = Р(А) + Р(В). Б Р(А+В) = Р(А) + Р(В) – Р(АВ). В Р(А+В) = Р(А) • Р(В). Г Р(А + В) = РВ(А) • Р(А).
4 Імовірність влучення в мішень під час одного пострілу дорівнює 0,8. За якою формулою обчислюється ймовірність того, що при 900 пострілах в мішень буде влучено 125 разів? А Формула Бернуллі: Б Формула Лапласа: В Формула Пуассона: Г 5 Як знаходиться ймовірність попадання випадкової величини в заданий інтервал (a; b) за допомогою функції розподілу? А Б В 6 Для яких випадкових величин застосовується інтегральна функція розподілу? А Дискретних. Б Неперервних. В Дискретних і неперервних. Г Тільки неперервних.
Частина друга 1Теорема про ймовірність появи хоча б однієї події та її частинний випадок. 2Прядильниця обслуговує 1000 веретен. Імовірність обривання нитки на одному веретені протягом однієї хвилини дорівнює 0,002. Знайти ймовірність того, що протягом однієї хвилини обривання виникне більше, ніж на трьох веретенах. 3Випадкова величинаХзадана щільністю розподілу:
Знайти математичне сподівання випадкової величини Х. 4Математичне сподівання швидкості повітря на даній висоті дорівнює 36 км/год. Середнє квадратичне відхилення дорівнює 6 км\год. Які швидкості повітря на цій висоті можна очікувати з імовірністю не меншою за 0.9? Розв`язання Тестова частина
Частина друга 1Теорема про ймовірність появи хоча б однієї події та її частинний випадок.
Теорема.Імовірність появи хоча б однієї з подій
Доведення:Позначимо через А подію, що полягає в появі хоча б однієї з подій
Із цього випливає, використовуючи теорему множення, що
або Частинний випадок. Якщо події
2Прядильниця обслуговує 1000 веретен. Імовірність обривання нитки на одному веретені протягом однієї хвилини дорівнює 0,002. Знайти ймовірність того, що протягом однієї хвилини обривання виникне більше, ніж на трьох веретенах. Розв`язання.Відповідно доумови задачі маємо n = 1000, p = 0,002,
Оскільки n велике, а p мале, то застосовуємо формулу Пуассона:
Отже,
3Випадкова величинаХзадана щільністю розподілу:
Знайти математичне сподівання випадкової величини Х. Розв`язання.Скористаємося формулою для знаходження математичного сподівання:
4Математичне сподівання швидкості повітря на даній висоті дорівнює 36 км/год. Середнє квадратичне відхилення дорівнює 6 км\год. Які швидкості повітря на цій висоті можна очікувати з імовірністю не меншою за 0.9? Розв`язання.Скористаємося нерівністю Чебишева:
Швидкість повітря буде визначати нерівність
Після перетворень отримаємо інтервал швидкості повітря:
Невідоме значення відхилення
Таким чином, шуканий інтервал швидкості повітря дорівнює
Поиск по сайту: |
 Р(А)
Р(А) 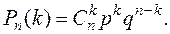

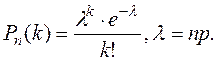
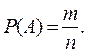
 .
.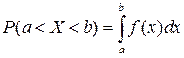 .
.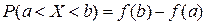 .
.
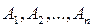 , незалежних у сукупності, дорівнює різниці між одиницею та добутком імовірностей протилежних подій
, незалежних у сукупності, дорівнює різниці між одиницею та добутком імовірностей протилежних подій  :
: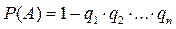 .
.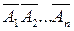 (жодна з подій не мала місце) протилежні, отже, сума їх імовірностей дорінює одиниці:
(жодна з подій не мала місце) протилежні, отже, сума їх імовірностей дорінює одиниці: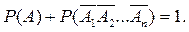

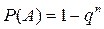 .
.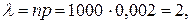 k > 3.
k > 3.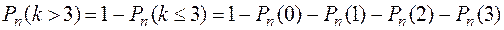 .
. .
.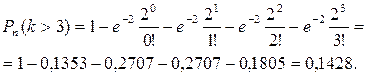
 .
.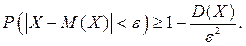

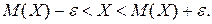
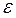 знайдемо, підставляючи в нерівність Чебишева
знайдемо, підставляючи в нерівність Чебишева