|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Для сжато-изгибаемого элемента на устойчивость
R m φeF – N ≥ 0; (2.39)
по деформативности
∆ f – [ ε ] ≤ 0 (2.40)
и другие. Здесь N – продольная сила; φ – коэффициент продольного изгиба; W – момент сопротивления сечения относительно соответствующих осей; М – изгибающий момент; с – коэффициенты для расчета на прочность с учетом развития пластических деформаций при изгибе; m – коэффициент условий работы; f – прогиб; [ε ] – предельная деформация или перемещение. В зависимости от вида целевой функции и ограничений используются методы линейного или нелинейного программирования. При линейной целевой функции и ограничениях чаще всего используется симплекс-метод и его модификации. Окончательно задача математического программирования для проведения оптимизационного поиска имеет вид: минимизировать (максимизировать)
f (x) → min (max);
при ограничениях
h i (x) = 0 i = 1,…, J, (2.41)
g j (x) ≥ , ≤ 0 j = 1,…,.J, (2.42)
x k (4) ≥ x k ≥ x k( 2) k = 1,…, J. (2.43)
При создании сварных конструкций необходимо обеспечить два основных противоречивых требования: обеспечить надежность и прочность конструкции и наибольшую экономию материалов. Задача оптимизации параметров балки по минимуму массы – задача математического программирования, она требует наличия двух компонентов: целевой функции, соответствующей выбранному критерию оптимальности, и системы ограничений, описывающей условия работы балки. В качестве критерия оптимизации следует выбрать массу балки mБ. Целевая функция
mБ → min
или L mБ = ρ ∫ F (x) dx → min,
где ρ – плотность материала балки; L – длина проектируемой балки; F(x) – функция изменения площади поперечного сечения балки по ее длине; х – координата положения сечения по длине балки. Изменение F по длине балки при условии минимизации ее массы соответствует распределению МИЗГ по длине. Поэтому многие элементы конструкций имеют переменную по длине форму поперечного сечения. Для создания конструкции балки минимальной массы необходимо уметь определять параметры поперечного сечения балки, имеющей минимальную площадь. Тогда в качестве целевой функции необходимо использовать F → min при известном законе распределения напряжений по сечению балки. Система ограничений выражается в виде следующих условий: -требования по прочности, устойчивости, жесткости, деформативности и т.п.; -габаритные ограничения для искомых параметров конструкции; -ограничения на сортамент проката, марки стали, соединения; -ограничения на условия изготовления, монтажа или эксплуатации конструкции. Пусть требуется найти размеры сечения коробчатого элемента минимальной площади при заданных изгибающих моментах относительно осей х и у поперечного сечения ( М х и М у ) и известных расчетном сопротивлении материала балки и коэффициенте условий работы m. Для простоты примем, что условия устойчивости балки, стенок и пояса выполняются. По условию жесткости высота балки не должна превышать размера Н и быть менее Н1. Для упрощения рассмотрим действие только двух моментов М у и М х и примем δС = δП = δ (рис.2.42). Площадь сечения
F = bh – (b - 2δ) (h - 2δ). (2.44)
bh 3 – (b - 2δ) (h - 2δ) 3
6h
b3h – (b -2δ) 3 (h - 2δ)
6b
δП
δ
Рис.2.42.К определению размеров коробчатого сечения
Сформулируем задачу оптимизации: при заданной толщине δ листового проката найти значения b и h, при которых площадь сечения F достигает минимума, причем выполняются следующие условия:
6 M X h 6 MYb
bh 3 – (b- 2δ) (h - 2δ) 3 hb3 – (h - 2δ) (b - 2δ) 3
h < H, (2.46)
h > H1. (2.47)
Эта задача относится к классу задач нелинейного программирования. Ограничение (2.45) определяет условие прочности, ограничение (2.46) – условие соблюдения габарита балки, ограничение (2.47) обусловливает деформативные свойства балки. Приведем геометрическую иллюстрацию рассматриваемого примера. При этом учтем дополнительные ограничения в соответствии с физическим смыслом задачи, так как переменные b и h не могут быть отрицательными:
b > 0; h > 0. (2.48)
На рис.2.43 кривая 1 соответствует ограничению (2.45), вертикальные прямые 2 – ограничению (2.46), 3 – ограничению (2.47), координатные оси – ограничениям (2.48). Огибающая ограничений отмечена штриховкой со стороны недопустимой области. В целевой функции для любого значения F переменные b и h связаны линейной зависимостью, так как
F = 2δ (b + h - 2δ).
Поэтому линии одинаковых уровней целевой функции ( на рис.2.43 показаны штриховыми линиями) представляют собой семейство параллельных прямых. Угол их наклона определяется из условия F = 0. Одна из линий этого семейства, касательная к огибающей ограничений , соответствует оптимальному значению целевой функции, а точка касания имеет координаты, равные оптимальному сочетанию b0 и h0 .
H1 h0 H h
F=0
Рис.2.43.Области ограничений в задаче оптимизации
В реальных условиях необходимо учитывать большое число ограничений и целевая функция может включать большое число переменных аргументов. Кроме того, математические модели ограничения по прочности могут иметь достаточно сложный для «ручного» способа расчета вид. Поэтому целесообразно задачи подобного рода решать на ЭВМ. Несущая способность балки характеризуется вполне определенным для каждой высоты сечения моментом сопротивления сечения W. В составных балках одно и то же значение W можно получить при различных вариантах компоновки сечения. Следует стремиться к тому, чтобы высота сечения h была оптимальной по расходу металла. Масса балки mБ находится в функциональной зависимости от высоты сечения:
mБ = f (h) → min.
Определим значение аргумента h, отвечающее минимальной величине функции mБ. Для этого функцию, как известно, необходимо исследовать на экстремум, т.е. найти ее первую производную и приравнять нулю. Масса балки равна сумме масс стенки и двух поясов:
mБ = mСТ + 2 mП. (2.49)
Масса стенки
mСТ = ρ hСТ δСТ L ψСТ, (2.50)
где ρ – плотность материала; L – длина балки; ψСТ > 1 – конструктивный коэффициент стенки, учитывающий превышение ее фактической массы над теоретической из-за наличия ребер жесткости, стыковых накладок, швов и т.п. Чтобы определить mП, надо предварительно найти площадь FП. Очевидно, изгибающий момент распределяется в поперечном сечении балки между поясами и стенкой пропорционально их моментам инерции. Тогда
MП JП
M J
откуда
МП = М с,
где МП – изгибающий момент, воспринимаемый поясами; JП –момент инерции сечения поясов; J – момент инерции всего сечения балки. С другой стороны (рис.2.44 )
МП = NП h,
следовательно, МП М с
hП hП
и NП М с
[σ ] hП [σ ]
Отсюда M c
hП [σ ]
где ψП – конструктивный коэффициент пояса.
h
Рис.2.44.Условия нагружения поясов балки
Полагая
hСТ ≈ hП ≈ h,
подставим (2.50) и (2.51) в (2.49):
М с
h [σ ]
Тогда первая производная
dm М с
dh h 2 [σ ]
или после сокращения на ρ L
М с
h 2 [σ ]
откуда
ψП М с
ψСТ [σ ]δСТ
Обозначим
ΨП
ΨСТ
Тогда
[σ ] δСТ δСТ
где k- коэффициент, зависящий от конструктивного оформления балки; при постоянном сечении для сварной балки k = 1,15; при переменном сечении для сварной балки k = 1,1. Так как вторая производная
d 2 m M c
dh 2 h3 [σ ]
то полученное значение h действительно отвечает минимуму функции m (h) и является оптимальным по расходу металла. Одновременно из (2.52)
М с
h [σ ]
т.е. mСТ = 2 mП. Таким образом, оптимальна та высота балки, при которой mСТ = 2 mП, или FСТ = 2 FП. Проведенный математический анализ является приближенным, так как он не учитывает изменения соотношения между высотой и толщиной стенки при различной высоте балки и, следовательно, не учитывает изменения коэффициента с. Между тем указанное соотношение играет не последнюю роль в вопросе экономичности балки: чем больше h / δСТ, тем выгоднее сечение. Однако в реальных условиях это отношение ограничивается необходимостью обеспечить прочность и устойчивость стенки, а также рядом других факторов. Поэтому обычно, меняя в формуле (2.53) δСТ, добиваются такой оптимальной высоты балки, при которой выдерживаются установленные практикой проектирования отношения h / δСТ. Оптимальная форма сечения двутавровой сварной разрезной подкрановой балки определяется в известной мере величиной
h ст
δ ст
При λ ст < 80 поперечные ребра жесткости ставятся по конструктивным соображениям и устойчивость стенки обеспечена даже при их отсутствии. В диапазоне 80 < λ ст < 150 поперечные ребра необходимы для обеспечения устойчивости стенки. Наконец, при λ ст > 150 требуется постановка, помимо поперечных ребер, также и продольного ребра. Сечение балки должно удовлетворять всем условиям прочности и деформативности в соответствии со СНиП II – В.3-82. Кроме того, должны быть выдержаны конструктивные требования. Предполагается, что задана марка стали, ее расчетные сопротивления и все коэффициенты, необходимые для расчета, а также расчетные усилия от вертикальной и горизонтальной нагрузок. Из числа конструктивных требований для рассматриваемой задачи выделим три основных ограничения: а) ограничение балки по высоте
h ст ≤ h стмакс , (2.55)
где величина h стмакс определяется габаритом балки, условиями транспортабельности или условиями применяемого сортамента металла; б) ограничение толщины стенки
δ ст ≥ δ стмин , (2.56)
где наименьшая толщина стенки δ стмин устанавливается по конструктивным соображениям; в) ограничение ширины поясных листов
b1 п ≤ c δ1п; b2 п ≤ c δ2п ,
где b 1 п, δ 1п – ширина и толщина верхнего пояса; b 2п , δ 2п – то же, нижнего пояса;
R – основное расчетное сопротивление.
Сечение балки должно удовлетворять следующим четырем условиям прочности: а) прочность стенки на смятие n1P
δ ст z
где n1 – коэффициент перегрузки; Р – вертикальное давление катка крана без учета коэффициента динамичности; m – коэффициент условий работы;
δ ст
Полагая σ см = mR, находим наименьшую толщину стенки по условию смятия:
JП 3,25 mR
б) прочность стенки на срез
ξ Q
h ст δ ст
где Q – наибольшая поперечная ила с учетом коэффициента динамичности; R с р – расчетное сопротивление срезу;
S h ст
J
S – статический момент полусечения; J – момент инерции поперечного сечения. Тогда наименьшая толщина стенки по условию восприятия касательных напряжений:
ξ Q
λ ст m R СР
в) прочность верхнего пояса
M MY N
W1 WY F1
г) прочность нижнего пояса
M
W2
где М – наибольший изгибающий момент; W1 и W2 – соответствующие моменты сопротивления сечения балки. Условие прочности при τ > 0,4 R
4 2R 2
в подкрановых балках всегда выполняется, поэтому специальная проверка этого условия не нужна. Вопросы, связанные с местной устойчивостью стенки, не анализируются. Расчет по второму предельному состоянию ( по деформациям) ограничивает величину наибольшего прогиба:
f 5 σx1 L f
δ ст 24 E h ст L
Здесь σх1 – напряжение верхнего пояса от вертикальной нагрузки без учета коэффициентов перегрузки n и динамичности 1 + μ.. Полагая приближенно
mR
ψ
находим минимальную по условиям деформативности высоту сечения:
mR L L
10 4 ψ f
Отсюда определяется минимальная толщина стенки по условию прогиба:
h МИН
λ ст
Определим условие, при котором балка имеет наименьший вес. При этом будем исходить из упрощенной схемы симметричного двутаврового стержня, испытывающего чисто изгибную деформацию (рис.2.45). Площадь поперечного сечения
F = δ ст h ст + 2 F1,
а момент сопротивления
δ стh ст2
δ ст
h F1
Рис.2.45.Симметричное сечение двутавра
Исключая площадь полки F1 из этих двух соотношений и заменяя h на λ ст δ ст, получаем 2 2W
3 λ ст δ ст
Здесь момент сопротивления можно считать величиной постоянной, так как всегда выполняется приближенное соотношение
M
Поиск по сайту: |

 WX = ,
WX = , WY = .
WY = .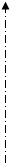 у
у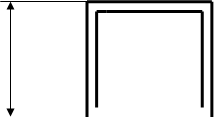
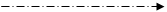 h x
h x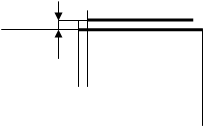


 С
С b
b


 + ≤ R k y. (2.45)
+ ≤ R k y. (2.45)

 b
b





 огранич.(3)
огранич.(3)



 огранич. (2)
огранич. (2)





 b0 огранич. (1)
b0 огранич. (1)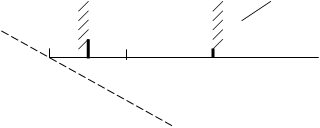


 NП = =
NП = = mП = ρ FП L ψП = ρ L ψП, (2.51)
mП = ρ FП L ψП = ρ L ψП, (2.51)



 NП
NП

 hСТ hП МП
hСТ hП МП NП
NП
 m = ρ h δСТ L ψСТ + 2 ρ L ψП.
m = ρ h δСТ L ψСТ + 2 ρ L ψП.



 hОПТ = 2 .
hОПТ = 2 .






 = 4 ρ L ψП > 0,
= 4 ρ L ψП > 0, ρ δСТ L ψСТ = 2 ρ L ψП,
ρ δСТ L ψСТ = 2 ρ L ψП,
 λ ст = = const. (2.54)
λ ст = = const. (2.54)
 с = 30 2,1 / R ; (2.57)
с = 30 2,1 / R ; (2.57) σ СМ = ≤ mR, (2.58)
σ СМ = ≤ mR, (2.58)
 3 JП
3 JП z = 3,25 .
z = 3,25 .
 a n1P
a n1P
 δ ст СМ = а ; а = ; (2.59)
δ ст СМ = а ; а = ; (2.59) τ = ≤ m R СР, (2.60)
τ = ≤ m R СР, (2.60)


 δ ст СР = ; (2.61)
δ ст СР = ; (2.61)

 3 σ 2
3 σ 2
 σ 2 + 3 τ 2 1 - ≤ R
σ 2 + 3 τ 2 1 - ≤ R 


 = ≤ . (2.64)
= ≤ . (2.64)

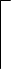
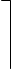

 h МИН = . (2.66)
h МИН = . (2.66)

 F1
F1