|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ ПОТЕРИ НАПОРА ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ
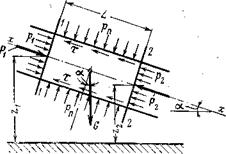
Исследуем равномерное движение потока жидкости — напорное (движение в трубопроводах) или безнапорное (движение в открытых каналах). Поскольку в этом случае средние скорости во всех поперечных сечениях одинаковы, местные сопротивления отсутствуют и существуют только сопротивления, проявляющиеся по длине потока, вызывающие соответствующие потери напора на трение. Чтобы получить общее выражение для этих потерь, рассмотрим поток жидкости с равномерным движением, ось которого наклонена к горизонту под углом a (рис. 4.3). Выделим в этом потоке двумя сечениями 1-1 и 2-2 некоторый объем малой длины Lи применим к его движению теорему теоретической механики о движении центра масс. Так как движение жидкости равномерное, ускорение центра масс выделенного объема равно нулю. Следовательно, сумма проекций всех внешних сил, приложенных к указанному объему, на любую ось также должна быть равна нулю. Такими внешними силами являются: силы давления Р\ и Р2 в сечениях 1-1 и 2-2, нормальные к этим сечениям и направленные: первая — в сторону движения, вторая — в сторону, обратную движению; эти силы равны произведению средних гидродинамических давлений в этих сечениях р1 и р2 на площадь сечения потока F, а именно: Р1 = р1F; Р2 = p2 F; силы гидродинамического давления на боковую поверхность рассматриваемого объема со стороны окружающей его жидкости рп, направленные нормально к этой поверхности; сила тяжести (вес объема, ограниченного сечениями 1-1 и 2-2), направленная по вертикали вниз и определяемая выражением G =rgFL; сила сопротивления движению Т. Сделаем допущение, что все частицы жидкости движутся с одинаковыми скоростями, равными средней скорости потока. Тогда сила сопротивления будет равна силе трения, возникающей на боковой поверхности выделенного объема. Для ее определения обозначим силу трения, приходящуюся на единицу поверхности (т. е. касательное напряжение), t. При этом полная сила трения
T=tAL где А — смоченный периметр того же объема, между сечениями 1-1 и 2-2. Эта сила направлена параллельно оси потока в сторону, обратную течению.
P1 –P2+Gsina - T=0 Подставив в это уравнение установленные выше выражения отдельных сил и приняв во внимание, что sina=(z1 — z2)/L, будем иметь
р1F- р2F+rgFL (z1 — z2)/L-tAL =0
Рис. 4.3 Разделив затем полученное уравнение на rgF с учетом того, что А/F = R (где R. — гидравлический радиус сечения), преобразуем его следующим образом:
z1+ p1 /rg = z2+ p2 /rg + (t/rg) (L/R) Сравнивая уравнение (4.4) и уравнение Бернулли в его обычной форме (3.25), составленное также для равномерного движения (v1=v2), приходим к следующему общему выражению для потери напора по длине потока: h тр = (t/rg) (L/R) ,(4.5) которое называют также основным уравнением равномерного движения. Рассмотрим наиболее интересный и важный для нас случай движения жидкости в напорном трубопроводе круглого сечения. При этом поступим следующим образом. Обозначим r внутренний радиус трубы и выберем начало координат в центре ее поперечного сечения О, направив ось x по оси трубы, а ось z по вертикали (рис. 4.4). Выделим затем внутри трубы объем жидкости в виде цилиндра, радиус которого у, длина L, и применим к нему основное уравнение (4.5). Поскольку гидравлический радиус круглого сечения К=у/2, это уравнение получит здесь следующую форму записи: h тр = (t/rg) (2L/у) ,. (4-.6) В частном случае, когда труба горизонтальна (z1=z2), уравнение (4.6) можно записать также в виде: h тр = Dp/rg = 2tL/rgу
где Dp — падение (перепад) давления на участке L. Отсюда для единичной силы трения (касательного напряжения) на радиусе у имеем
t = Dpу/2L (4.8)
Рис. 4.4 Полученное выражение позволяет установить закон распределения касательных напряжений в поперечном сечении трубы. Из него видно, что t изменяется по линейному закону: наименьшее его значение tо = 0 будет на оси трубы (при у = 0), а наибольшее — у ее стенок (при у = r) : t r = Dpr/2L (4.9) График изменения t по сечению трубы представлен на рис. 4.4 (справа). Здесь уместно подчеркнуть, что основное уравнение равномерного движения (4.5), равно как и общие выражения для определения потери напора (4.6) и перепада давления (4.7) в круглой трубе, а также закон распределения касательных напряжений по сечению трубы, выражаемый зависимостью (4.8), в одинаковой степени применимы как для ламинарного, так и для турбулентного режима. Если принять далее, как это было предложено Шези на основе опытов 1775 г., величину t/rg пропорциональной квадрату скорости, а коэффициент пропорциональности обозначить (1/С)2, т. е. принять, что t/rg = (1/С2)v2, то из уравнения (4.6) получим: h1-2 = v2 L/C2R (4.10)
С учетом того, что hтр/L = i (где i — гидравлический уклон), из выражения (4.10) получается следующая формула для скорости при равномерном движении жидкости:
Ее обычно называют формулой Шези. Значения коэффициента С в формуле (4.11) определяют опытным путем. Величина С2 имеет размерность ускорения. Для практического применения, однако, эмпирические коэффициенты удобнее иметь безразмерными. Поэтому коэффициент Шези С впоследствии был заменен
где l — безразмерная величина, обычно называемая коэффициентом гидравлического трения или гидравлического сопротивления. Такая замена позволяет привести формулу (4.10) к очень удобному для практического пользования виду:
h1-2 = l( L/4R)(v2/2g) (4.13) Поскольку для круглых труб 4R =d, то из уравнения (4.13) получаем так называемую формулу Дарси—Вейсбаха для определения потерь напора при равномерном движении жидкости в круглых трубах: h1-2 = l( L/d)(v2/2g) (4.14) Формулы (4.11) и (4.14) являются наиболее распространенными для определения потерь напора. Первую из них применяют главным образом при расчетах открытых потоков, а вторую— напорных (в круглых трубах).
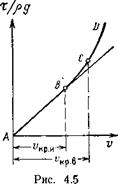
Нетрудно видеть, что формулы (4.10) и (4.14) принципиально ничем не отличаются, потеря напора в них выражается, по существу, в одной и той же форме - пропорционально квадрату средней скорости. Поэтому закон сопротивления, устанавливаемый этими формулами, принято называть законом квадратичного сопротивления, а сами формулы — квадратичными. Более поздние исследования показали, что на потерю напора помимо скорости оказывает существенное влияние ряд факторов (характер режима, форма и размеры сечения, вязкость жидкости, материал и состояние стенок), не учитываемых в явном виде формулами Шези и Дарси—Вейсбаха. Исследования выявили также, что в действительности квадратичный закон сопротивления подтверждается далеко не во всех случаях движения жидкости и касательное напряжение пропорционально квадрату скорости в случае турбулентного режима только при достаточно больших числах Рейнольдса. В остальных случаях турбулентного режима т будет пропорционально скорости в степени, несколько меньше второй, а при ламинарном режиме — пропорционально скорости лишь в первой степени. Поэтому в общем случае следовало бы принять t/rg = bvn (4.18) где b — некоторый коэффициент пропорциональности; п — показатель степени, при ламинарном режиме п=1 а при турбулентном всегда п> 1 и зависит от числа Рейнольдса. На рис. 4.5 представлена графическая интерпретация уравнения (4.18). График построен на основании опытов Рейнольдса в координатных осях v и t/rg . Прямая АВ н,а графике соответствует ламинарному режиму, а кривая СD — турбулентному. Участок кривой между точками В и С характеризует переходную зону. Однако квадратичные формулы Шези и Дарси—Вейсбаха очень удобны для практических целей, целесообразны с точки зрения единообразия расчета и обычно применяются как для турбулентного, так и для ламинарного режима. Отклонения же от квадратичного закона учитываются тем, что коэффициенты l и С ставятся в косвенную зависимость от скорости. Таким образом, эти формулы устанавливают только общую форму закона сопротивлений. Для определения численного значения потери напора необходимо в каждом отдельном случае учесть еще и влияние всех указанных выше факторов. Этой цели служат специальные формулы для коэффициентов lи С.
Поиск по сайту: |
 Составим сумму проекций всех перечисленных сил на ось xx, параллельную оси потока. С учетом того, что силы рп не дают проекции на указанную ось, получим
Составим сумму проекций всех перечисленных сил на ось xx, параллельную оси потока. С учетом того, что силы рп не дают проекции на указанную ось, получим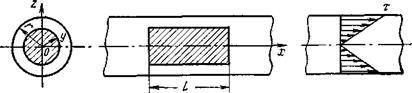
 v= С ÖRi (4.11)
v= С ÖRi (4.11) С = Ö 8g/ l (4.12)
С = Ö 8g/ l (4.12)