Закономерность движения жидкостей и газов по трубопроводам. Уравнение Бернулли. Гидравлическое сопротивление трубопроводов, метод расчета.

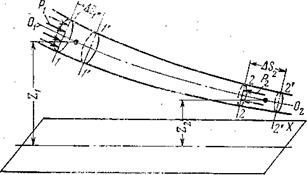
Уравнение Бернулли является основным в технической гидромеханике. Оно устанавливает зависимость между скоростью и давлением в различных сечениях одной и той же элементарной струйки.

При выводе этого уравнения ограничимся случаем установившегося медленно изменяющегося движения.

Выделим в пространственной элементарной струйке объем, ограниченный в некоторый момент времени tсечениями 1—/ и 2—2, нормальными к оси струйки O1-O2 (рис. 3.10). Первоначально будем считать жидкость идеальной, т. е. лишенной вязкости. Силы внутреннего трения в такой жидкости отсутствуют и к выделенному объему струйки приложены только силы тяжести и силы гидродинамического давления. Пусть за некоторый малый промежуток времени dtуказанный объем переместится в положение Г-Г и 2'-2'. Применим к его движению теорему кинетической энергии, согласно которой приращение кинетической энергии движущейся системы материальных частиц равно сумме работ всех сил, действующих на систему. Эта теорема может быть выражена следующим простым уравнением:

DW = S А

(3.11)

где DW— приращение кинетической энергии; S А — сумма работ действующих сил.

Рис. 3.10*.

В рассматриваемом случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т. е. как разность кинетической энергии объема V_1’-2’ и объема V _1-2. Замечая, что объем V_1’-2 входит как составная часть в выражения для объемов V _1-2 и V_1’-2’

V _1-2 = V_1-1’ + V_1’-2;

V_1’-2’= V_1’-2+ V_2-2’

и имея в виду, что кинетическая энергия объема V_1’-2при установившемся движении жидкости одинакова как в момент времени t, так и в момент t + dt, приходим к выводу: искомое приращение кинетической энергии в конечном счете определяется разностью кинетической энергии объемов V_2-2’ и V_1-1’. Названные объемы есть результат перемещения за время dtторцовых сечений выделенного участка элементарной струйки. Обозначив v₁ и v_{2 ,} скорости в сечениях 1-1 и 2-2 найдем, что соответствующие перемещения будут равны v1dt и v₂ dt, а рассматриваемые объемы:

V_1-1’=dF₁v₁dt=dQ₁dt; V_2-2’=dF₂ v₂dt=dQ₂dt;где dQ₁ и dQ₂ — значения расхода в сечениях 1-1 и 2-2.

Но по условию неразрывности расход во всех сечениях элементарной струйки одинаков (dQ₁= dQ₂ = dQ) и, следовательно, V_1-1’ = V_2-2’ =. dQdt Масса же рассматриваемых объемов rdQdt.

.

Таким образом, выражение для приращения кинетической энергии можно записать в виде

D W=rdQdt. V₂²= rdQdt V₁²;

2 2

или

DW=dm V₂² - dm V₁²= dm(V₂²- V₁²)

2 2 2

Перейдем теперь к определению работы сил, действующих на рассматриваемый объем жидкости. Работа силы тяжести равна произведению этой силы на путь, пройденный точкой ее приложения, т. е. центром массы (тяжести) движущегося объема жидкости по вертикали. Рассматривая, как и ранее, выделенный объем струйки в двух его положениях состоящим из объема V_1’-2 и равных между собой объемов V_1-1’ - и V_2-2’, легко прийти к заключению, что работа A_т сил тяжести будет равна произведению силы тяжести объема V_1-1’- на расстояние по вертикали между центрами масс объемов V_1-1’ - и V_2-2’, т. е.

A_т= dmgz₁- dmgz₂=dmg(z₁-z₂)

где z₁ и z₂ — расстояния по вертикали от произвольной горизонтальной плоскости, называемой плоскостью сравнения, до центров масс объемов V_1-1’ - и V_2-2’, иначе говоря, вертикальные координаты центров масс этих объемов.

Силы давления, действующие на объем жидкости, складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы во все время движения нормальны к перемещению их точек приложения. Сумма работ сил давления S А_д на торцовые сечения составляет

S A_д =p₁dF₁dS₁- p₂dF₂dS_2.

где p₁dF . p₂dF₂ — силы давления на торцы /-/ и 2-2; dS₁, dS₂ — элементарные перемещения точек приложения этих сил за время dt ( работа сил давления на торец 2 отрицательна, так как направление силы p₂dF₂ противоположно перемещению dS₂ ) .

Но величины dF₁dS₁ и dF₂dS₂ есть равные между собой объемы V_1-1’ и V_2-2’ массы dm. Поэтому с учетом того, что dт =p V_1-1’= р V_2-2’ , выражение для суммы A_Д можно представить в виде

A_Д = (dm/r)(р₁ —р₂).

Подставив найденные выражения для работ сил и для приращения кинетической энергии в уравнение (3.11), получим:

dm(V₂²- V₁²)= dmg(z₁-z₂)+ (dm/r)(р₁ —р₂).

Разделим затем это уравнение на dт =rdQdt, т. е. отнесем его к единице массы протекающей жидкости, и перегруппируем члены. Будем иметь

gz₁ + p₁/r + V₁²/2 = gг₂ + p₁/r + V₂² /2. (3.12)

Учитывая, что сечения 1-1 и 2-2 взяты нами произвольно, это уравнение можно распространить на всю струйку, применив его для любых поперечных сечений, взятых по ее длине, и представить в более общем виде:

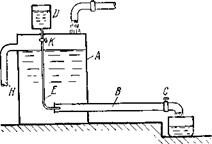
gz₁ + p/p + V²/2 = сопst.

Уравнения (3.12) и (3.13) представляют собой разную запись уравнения Бернулли для элементарной струйки идеальной жидкости. Сумму трех слагаемых, входящих в уравнение (3.13), называют полной удельной энергией жидкости в данном сечении струйки и обозначают э . Различают удельную энергию положения gг, удельную энергию давления р/р и кинетическую удельную энергию V²/2.

В соответствии с этим уравнение Бернулли можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т. е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии есть величина постоянная во всех сечениях струйки.

РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ

Одна из основных задач практической гидравлики — оценка потерь напора на преодоление гидравлических сопротивлений, возникающих при движении реальных жидкостей в различных гидравлических системах. Точный учет этих потерь во многом определяет надежность технических расчетов, степень совершенства и экономическую целесообразность инженерных решений, принимаемых при проектировании.

Чтобы правильно определить эти сопротивления, прежде всего необходимо составить ясное представление о механизме самого движения жидкости. При исследовании вопроса приходим к заключению о существовании двух различных, резко отличающихся режимов движения. Это было известно еще в первой половине XIX в., но со всей очевидностью наличие двух режимов движения было подтверждено только в 1883 г. известным физиком Рейнольдсом на основе весьма простых и наглядных опытов.

Сущность этих опытов сводится к следующему. Имеется бак А, к которому присоединена горизонтальная стеклянная труба В, снабженная краном С (рис. 4.1). Над баком устанавливается сосуд D с окрашенной жидкостью, подаваемой в трубу В по тонкой трубке Е. Перед проведением опытов бак заполняют водой (например, из водопровода через трубу F), и ее уровень поддерживают постоянным при помощи сливной линии H. Затем, открывая кран С, в трубе В создают поток жидкости, а открывая кран К на трубе Е, в этот поток подают тонкую струю окрашенной жидкости.

Постепенно все более открывая кран С, можно повышать расход, и, следовательно, скорость течения жидкости в трубе В. При этом можно наблюдать следующую картину: при небольших скоростях течения в трубе В окрашенная жидкость движется в виде отчетливо выраженной тонкой струйки (рис. 4.2, а), не смешиваясь с потоком неокрашенной воды; при повышении скорости течения окрашенная струйка начинает колебаться и принимает волнообразные очертания. Затем на отдельных ее участках начинают появляться разрывы, она теряет отчетливую форму и, наконец, при каком-то определенном значении скорости полностью разрывается, целиком размываясь жидкостью (рис. 4.2,6). При этом отдельные частицы красящего вещества смешиваются со всей массой жидкости, равномерно ее окрашивая.

Если в этом случае подмешать в поток жидкости мелкие твердые частицы такой же плотности, что и сама жидкость, перемещение этих частиц будет происходить по весьма сложным криволинейным траекториям.

При проведении опыта в обратном порядке, т. е. при постепенном закрытии крана, наблюдаемые явления повторяются

в обратном порядке, но обычно при несколько других значениях скоростей.

Движение жидкости при малых скоростях, когда отдельные струйки жидкости движутся параллельно оси потока, называют ламинарным (от латинского слова «ла-мина» — слой), или струйчатым. Ламинарное движение можно рассматривать как движение отдельных слоев жидкости, происходящее без перемешивания частиц.

Второй вид движения жидкости, наблюдаемый при больших скоростях, называют турбулентным («турбулентус» по-латински— вихревой). В этом случае в движении жидкости нет видимой закономерности. Отдельные частицы перемешиваются между собой и движутся по самым причудливым, все время из-

Рис. 4.2

меняющимся траекториям. Такое движение также называют беспорядочным. В действительности, однако, и при турбулентном режиме имеют место определенные закономерности.

ЧИСЛО РЕЙНОЛЬДСА

Обобщив результаты своих опытов, проведенных на круглых трубах, а также исходя из некоторых теоретических соображений, Рейнольдс нашел общие условия, при которых возможны существование того или иного режима и переход от одного режима к другому. Он установил, что основными факторами, определяющими характер режима, являются: средняя скорость движения жидкости v, диаметр трубопровода d, плотность жидкости r, ее абсолютная вязкость m. При этом чем больше размеры поперечного сечения и плотность жидкости и чем меньше ее вязкость, тем легче, увеличивая скорость, осуществить турбулентный режим.

Для характеристики режима движения жидкости Рейнольде ввел безразмерный параметр Ке, учитывающий влияние перечисленных выше факторов, называемый числом (или критерием) Рейнольдса.

Rе = vdr/m. (4.1)

Так как m /r = n , формулу (4.1) можно записать в виде

Rе = vd/ n . (4.2)

Границы существования того или иного режима движения жидкости определяются двумя критическими значениями числа Рейнольдса: нижним Rе кр.н. и верхним Rе_кр. _в- Значения скорости, соответствующие этим значениям числа Рейнольдса, также называют критическими. При Rе<Rе кр.н. возможен только ламинарный режим, а при Rе> Re кр.в — только турбулентный; при Rе кр.н. <Rе< Re кр.в наблюдается неустойчивое состояние потока. Таким образом, для определения характера режима движения жидкости необходимо в каждом отдельном случае вычислить по формуле (4.2) число Рейнольдса и сопоставить результат с критическими значениями.

В опытах самого Рейнольдса были получены следующие значения: Rе кр.н. = 2000, Re кр.в= 12 000. Многочисленные эксперименты, проведенные в более позднее время, показали, что критические числа Рейнольдса не являются вполне постоянными и в действительности при известных условиях неустойчивая зона может оказаться значительно шире.

В настоящее время при расчетах принято исходить только из одного критического значения числа Рейнольдса — Rе кр. = 2300. При Rе<2300 режим всегда считается ламинарным, а при Re>2300 — всегда турбулентным. При этом движение жидкости в неустойчивой зоне исключается из рассмотрения, что приводит к некоторому запасу и большей надежности в гидравлических расчетах.

Без особого труда могут быть получены значения Rе также для сечения любой формы, не только круговой. Имея в виду, что при круговом сечении гидравлический радиус R =d/4, подставим в формулу (4.2) вместо d его значение, равное 4R. Тогда получим формулу для числа Рейнольдса, выраженного через гидравлический радиус:

Rе = 4vR/ n, (4.3)

откуда

Rе/4=vR/n
Принимая по-прежнему для критического значения числа Рейнольдса независимо от формы живого сечения Rе кр. = 2300, находим, что для сечения любой формы критерием для суждения о характере режима движения является величина, равная 2300/4 = 575. Таким образом, если vR/n <575, режим ламинарный, если vR/n >575, режим турбулентный.

.

Поиск по сайту: