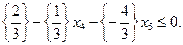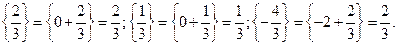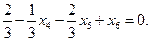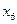|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Алгоритм метода Гомори
1. Решаем задачу симплекс методом. Если найденное решение целочисленно, то задача решена. Если задача не разрешима, то она не имеет решений и в целых числах. 2. Если среди компонент оптимального решения есть не целые, то надо выбрать компоненту с оптимальной целой частью и сформулировать правильное отсечение из условия 3. Вводим дополнительную неотрицательную целую переменную 4. Полученную расширенную задачу решаем симплекс-методом. Если новый найденный план целочисленный, то задача решена, если нет то повторяем процедуру. Замечание. Если задача разрешима в целых числах, то после конечного числа шагов (итераций) оптимальный целочисленный план будет найден. Если в процессе решения появится уравнение, выражающее основную переменную через неосновные, в котором свободный член не целый, а все остальные коэффициенты целые, то задача в целых числах решений не имеет. В симплекс таблице это условие соответствует тому, что в строке с нецелым свободным членом все остальные коэффициенты целые. Пример. Решить задачу в целых числах.
Приведем задачу к каноническому виду:
Построим симплекс-таблицу
Данный план не оптимален, так как в оценочной строке есть отрицательные элементы. Наибольший по модулю находится в столбце
Полученное решение не является оптимальным.
Полученное решение численным Построим правильное отсечение из условия:
Найдем дробные части от чисел стоящих в фигурных скобках:
Получим неравенство
Введем дополнительную целую переменную
Полученное уравнение необходимо добавить в систему ограничений и решить симплекс-методом новую задачу. Для сокращения числа шагов можно вводить новое уравнение в симплекс-таблицу, полученную на последнем шаге.
Полученное базисное решение не допустимо Замечание. Включение в систему ограничений дополнительного ограничения, соответствующего правильному отсечению всегда дает недопустимое базисное решение. Для получения допустимого базисного решения необходимо перевести в основные переменные переменную, входящую со знаком «+» в уравнение, в котором свободный член отрицательный. В рассматриваемом случае это переменная
Полученное решение является оптимальным. Найденный план целочисленный
Поиск по сайту: |
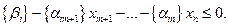
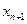 и получаем новое уравнение
и получаем новое уравнение 
 - дробная часть числа
- дробная часть числа 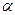 .
.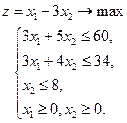
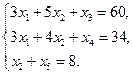
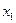

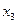
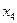
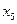
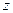
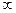
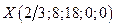 оптимально, но не является цело
оптимально, но не является цело .
.