 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Графический метод решения задачи линейного программирования
Рассмотрим ЗЛП в стандартной форме для случая двух переменных
Пусть система неравенств (10) совместна (имеет хотя бы одно решение). Любое неравенство этой системы геометрически определяет полуплоскость с граничной прямой Так как система совместна, то полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность всех этих точек называется многоугольником решений. Это может быть точка, отрезок, луч, прямая, замкнутый многоугольник, неограниченная многоугольная область. Решение ЗЛП геометрически представляет собой поиск такой точки многоугольника решений, координаты которой доставляют целевой функции наибольшее (наименьшее) значение. Причем допустимым решением являются все точки многогранника. Рассмотрим так называемую линию уровня целевой функции z, то есть линию, вдоль которой эта функция принимает одно и то же фиксированное значение Алгоритм решения задачи линейного программирования графическим методом (число переменных 1. Строится многоугольная область допустимых решений на плоскости
целевой функции z в любой точке 2. Прямая 3. Для нахождения координат оптимальной точки, надо решить систему уравнений, которая соответствует прямым, пересечение которых образует эту точку. Значение целевой функции в этой точке будет оптимальным, а сами координаты точки будут являться решением задачи ЛП. Пример. Решить геометрически задачу:
Построим многоугольник всех допустимых решений OABCD и направляющий вектор целевой функции
откуда
Максимум (максимальное значение целевой функции) равен:
Поиск по сайту: |
 :
: (9)
(9) (10)
(10)
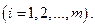 Условия не отрицательности определяют полуплоскости с соответственными граничными прямыми
Условия не отрицательности определяют полуплоскости с соответственными граничными прямыми  и
и  .
.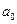 :
:  или
или 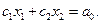
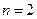 ).
). соответствующая ограничениям. Затем строится вектор-градиент
соответствующая ограничениям. Затем строится вектор-градиент
 область допустимых решений.
область допустимых решений. (линия уровня функции z), перпендикулярная вектору-градиенту, передвигается параллельно самой себе в направлении вектора-градиента в случае задачи на максимум (и в противоположном направлении - в случае задачи на минимум) до тех пор, пока она не покинет область допустимых решений. Предельная точка (или точки) области являются оптимальными точками.
(линия уровня функции z), перпендикулярная вектору-градиенту, передвигается параллельно самой себе в направлении вектора-градиента в случае задачи на максимум (и в противоположном направлении - в случае задачи на минимум) до тех пор, пока она не покинет область допустимых решений. Предельная точка (или точки) области являются оптимальными точками.
 (Рис. 1). Направление вектора-градиента указывает направление возрастания целевой функции. Так как рассматриваемая задача на отыскание максимума, то прямую, перпендикулярную вектору
(Рис. 1). Направление вектора-градиента указывает направление возрастания целевой функции. Так как рассматриваемая задача на отыскание максимума, то прямую, перпендикулярную вектору  перемещаем в направлении этого вектора параллельно самой себе до тех пор, пока эта прямая не покинет область допустимых решений. На границе области, в нашем случае в точке С, и будет решение задачи. Точка С находится на пересечении прямых
перемещаем в направлении этого вектора параллельно самой себе до тех пор, пока эта прямая не покинет область допустимых решений. На границе области, в нашем случае в точке С, и будет решение задачи. Точка С находится на пересечении прямых  и
и  . Следовательно, ее координаты определяются решением системы этих уравнений уравнении:
. Следовательно, ее координаты определяются решением системы этих уравнений уравнении: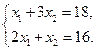
 т.е. точка С имеет координаты (6, 4).
т.е. точка С имеет координаты (6, 4).
 Ответ:
Ответ: 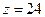 при оптимальном решении
при оптимальном решении