 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Примеры задач линейного программирования
Задача об использовании ресурсов.Для изготовления двух видов продукции
Прибыль, получаемая от единиц продукции Решение. Составим экономико-математическую модель задачи. Пусть
По смыслу задачи переменные:
Суммарная прибыль
Таким образом, получили экономико-математическую модель задачи: найти такой план выпуска продукции Задача составления рациона (задача о диете, задача о смесях).Имеются два вида корма I и II, содержащие питательные вещества (витамины)
Стоимость 1 кг корма I и II соответственно равна 4 и 6 руб. Необходимо составить такой дневной рацион, имеющий минимальную стоимость,в котором содержание каждого вида питательных веществ было бы не меньше установленного предела. Решение. Составим экономико-математическую модель задачи. Пусть
По смыслу задачи переменные:
Общая стоимость рациона z составит в руб.:
Таким образом, получили экономико-математическую модель задачи: составить дневной рацион
Поиск по сайту: |
 и
и  используется четыре вида ресурсов
используется четыре вида ресурсов  , Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 1:
, Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 1:



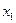 и
и  - число единиц продукции
- число единиц продукции  единиц ресурса
единиц ресурса  единиц ресурса
единиц ресурса 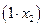 единиц ресурса
единиц ресурса  единиц ресурса
единиц ресурса  (3)
(3) (4)
(4)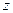 составит
составит  руб. от реализации продукции
руб. от реализации продукции  руб. от реализации продукции
руб. от реализации продукции  (5)
(5) , удовлетворяющий системе (3) и условию (4), при котором функция (5) принимает максимальное значение.
, удовлетворяющий системе (3) и условию (4), при котором функция (5) принимает максимальное значение. . Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ приведены в таблице 2:
. Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ приведены в таблице 2: единиц питательного вещества
единиц питательного вещества  единиц питательного вещества
единиц питательного вещества  единиц питательного вещества
единиц питательного вещества  (6)
(6) (2)
(2)