 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Двойственные задачи линейного программирования
Экономическая интерпретация двойственной задачи. Рассмотрим две задачи ЛП
Цены ресурсов
Свойства взаимно двойственных задач
1. В одной задачи ищется максимум, в другой минимум линейной функции. 2. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений другой задачи. 3. Каждая задача записана в стандартной форме, причем в задаче на минимум все неравенства вида « 4. Матрицы коэффициентов при переменных в системах ограничений обоих задач являются транспонированными друг к другу: 5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных другой задачи. 6. Условия неотрицательности переменных имеются в обеих задачах. Две задачи ЛП, обладающие этими свойствами называются симметричными взаимно двойственными (двойственными).
Поиск по сайту: |
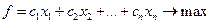

 и условиях неотрицательности
и условиях неотрицательности
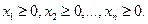 Составить такой план выпуска продукции
Составить такой план выпуска продукции  при котором прибыль от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдёт имеющихся запасов.
при котором прибыль от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдёт имеющихся запасов.
 и условиях неотрицательности
и условиях неотрицательности
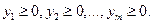 Найти такой набор цен оценок) ресурсов
Найти такой набор цен оценок) ресурсов 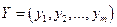 при котором общие затраты на ресурсы будут минимальны при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли от реализации этой продукции
при котором общие затраты на ресурсы будут минимальны при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли от реализации этой продукции
 -это цены на ресурсы, которые называются учетными, неявными, теневыми. Смысл этих названий состоит в том, что это условные «ненастоящие» цены, которые появились бы в том случае, если фирма, осуществляющая данный производственный процесс, вместо производства, решила бы продать имеющиеся ресурсы, причем таким образом, чтобы прибыль от их продажи была бы не меньше, чем прибыль от данного производственного процесса. А фирма, покупающая ресурсы, желала бы минимизировать затраты на покупку. В отличие от «внешних» цен
-это цены на ресурсы, которые называются учетными, неявными, теневыми. Смысл этих названий состоит в том, что это условные «ненастоящие» цены, которые появились бы в том случае, если фирма, осуществляющая данный производственный процесс, вместо производства, решила бы продать имеющиеся ресурсы, причем таким образом, чтобы прибыль от их продажи была бы не меньше, чем прибыль от данного производственного процесса. А фирма, покупающая ресурсы, желала бы минимизировать затраты на покупку. В отличие от «внешних» цен 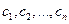 на продукцию, известных до начала производства, цены ресурсов
на продукцию, известных до начала производства, цены ресурсов 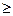 », а в задаче на максимум - вида «
», а в задаче на максимум - вида « 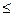 ».
». и
и 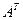 .
.