 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Появление вырожденного базисного решения
Рассмотрим задачу:
Решим задачу симплексным методом. Введем дополнительные переменные и составим симплекс-таблицу.
Так как полученное решение
Полученное решение
Решение При этом целевая функция не увеличилась, но и не ухудшилась. Выполненный шаг, хотя и не улучшил значение целевой функции, лишнем не является, так как привел к новому базисному решению. На практике, наличие пустых шагов может привести к зацикливанию задачи. Вывод. Если на каком-либо шаге симплекс-метода наибольшее возможное значение переменной достигается в нескольких уравнениях одновременно, то в качестве разрешающего можно выбрать одно из них (в симплекс-таблице совпадение оптимальных оценочных отношений). Тогда на следующем шаге получим вырожденное базисное решение, переход к очередному базисному решению может не изменить значение целевой функции. Замечание. Вырождение, полученное при оптимальном решении может привести к альтернативному оптимуму даже при нулевых коэффициентах при всех не основных переменных в целевой функции.
Отсутствие конечного оптимума. Рассмотрим задачу:
При геометрическом решении убеждаемся, что оптимум отсутствует. Рассмотрим симплекс-метод на очередном шаге:
Условие оптимальности целевой функции не выполнено, так как в строке целевой функции коэффициент при Вывод: если на каком либо шаге получается, что во всех уравнениях системы (строках симплекс-таблице) бесконечные оценочные отношения той переменной, которая переводится в основные, то задача не имеет конечного оптимума.
Поиск по сайту: |
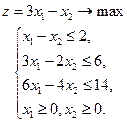
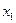

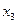
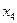
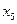
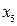
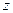
 не оптимально, переходим к новой симплекс-таблице. Причем, в качестве разрешающей строки можно взять как первую, так и вторую.
не оптимально, переходим к новой симплекс-таблице. Причем, в качестве разрешающей строки можно взять как первую, так и вторую.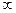
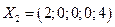 вырожденно, так как основная переменная
вырожденно, так как основная переменная  и вновь не является оптимальным. Переходим к новой симплекс-таблице.
и вновь не является оптимальным. Переходим к новой симплекс-таблице.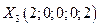 так же вырожденно, так как основная компонента
так же вырожденно, так как основная компонента 
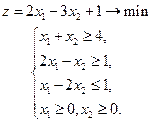
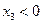 . При попытке ввести
. При попытке ввести 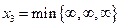 . Уравнения не ограничивают рост
. Уравнения не ограничивают рост