 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
проводимости термодинамическим методом ⇐ ПредыдущаяСтр 7 из 7
В реальном кристалле в переносе электричества обычно принимают участие несколько сортов носителей зарядов. Так в бинарном кристалле АВ, свободном от посторонних примесей, это могут быть ионы – катионы и анионы, электроны и дырки. Суммарная проводимость может быть записана выражением
где scat, san, se, и sh – катионная, анионная, электронная и дырочная проводимости, соответственно. Чтобы выделить вклад каждого из участников переноса, пользуются понятием числа переноса, которое представляет собой долю, вносимую каждым из них в общую проводимость.
Тогда Пусть кристалл находится в равновесном состоянии. Это означает, что общий градиент электрохимического потенциала в нем равен нулю. Между тем термодинамически неизбежно возникающие в таком кристалле точечные дефекты, внося локальную концентрационную неоднородность, одновременно вызывают локальные возмущения силового поля решетки и возникновение локальных электрохимических градиентов. Так, удаление ионов из катионной и анионной подрешеток кристалла АВ, порождая вакансии, должно привести к возникновению локальных градиентов
Точно так же беспорядок, проявляющийся в переходе электрона из валентной зоны в зону проводимости, в равновесном кристалле порождает локальные электрохимические градиенты
Запишем выражение для ионного тока. Очевидно, что
При суммировании в уравнении (7.20) было принято во внимание, что заряд катиона имеет знак «+», а аниона – «–». Примем, что Zcat = Zan, тогда, учитывая (7.18),
где sion= scat+ san. Если в уравнении (7.20) заменить
По аналогии, электронный ток, складывающийся из потока электронов и дырок, может быть выражен как
где sel = se+ sh. Общий ток в кристалле представляет собой сумму ионного и электронного токов:
Если, например, в кристалле АВ возникновение проводимости связано с ионизацией катиона:
то суммарную плотность тока можно представить как
Если же появление носителей зарядов идет за счет процесса
Пусть мы имеем дело с реакцией (7.22). Изменение электрохимического потенциала для нее можно записать как
В условиях равновесия
или, что то же самое,
В условиях равновесия суммарный ток IS равен нулю. Тогда из (7.24) получим
Уравнение (7.25) при наличии информации о
Значение
А так как
Поместим рассматриваемый кристалл МО в такие условия, чтобы равновесное давление кислорода с одной стороны кристалла было равно
Поиск по сайту: |

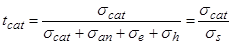 ,
, .
. . Из чего следует, что
. Из чего следует, что  . Информация о числах переноса или, что то же самое, о вкладе ионной, электронной и дырочной составляющих в суммарную проводимость кристалла имеет большое практическое значение. Она может быть получена из термодинамических данных, характеризующих равновесие дефектов в кристалле.
. Информация о числах переноса или, что то же самое, о вкладе ионной, электронной и дырочной составляющих в суммарную проводимость кристалла имеет большое практическое значение. Она может быть получена из термодинамических данных, характеризующих равновесие дефектов в кристалле. и
и  , причем в условиях равновесия их сумма должна быть равна нулю
, причем в условиях равновесия их сумма должна быть равна нулю . (7.18)
. (7.18)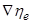 и
и  , сумма которых тоже равна нулю
, сумма которых тоже равна нулю . (7.19)
. (7.19)
 . (7.20)
. (7.20)



 (7.21)
(7.21)
 , (7.22)
, (7.22) . (7.23)
. (7.23) .
. , тогда
, тогда 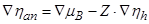 . Подставляя в (7.23), получим
. Подставляя в (7.23), получим
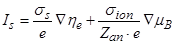 . (7.24)
. (7.24)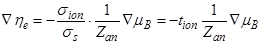 . (7.25)
. (7.25)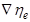 и
и  позволяет найти ионное число
позволяет найти ионное число  или, что то же самое, определить ионную составляющую в общей проводимости кристалла. Действительно, пусть мы имеем дело с оксидом типа МО, тогда
или, что то же самое, определить ионную составляющую в общей проводимости кристалла. Действительно, пусть мы имеем дело с оксидом типа МО, тогда  . В таком случае соотношение (7.25) с учетом того, что Zan = 2, приобретает вид
. В таком случае соотношение (7.25) с учетом того, что Zan = 2, приобретает вид . (7.26)
. (7.26) . Принимая, что
. Принимая, что  , получим
, получим  . Подставляя в (7.26), имеем
. Подставляя в (7.26), имеем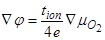 или
или  .
. , получим
, получим .T
.T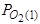 , а с другой стороны –
, а с другой стороны –  . Возникающий в результате этого градиент концентрации приведет к появлению разности потенциалов
. Возникающий в результате этого градиент концентрации приведет к появлению разности потенциалов  , измерив которую, находят
, измерив которую, находят  .
.