Выясним физический смысл коэффициента диффузии

;

,

где n/t – число элементарных скачков частицы в единицу времени. Введем величину t = t/n – время между очередными скачками частицы.

.

Таким образом коэффициент диффузии представляет собой отношение квадрата длины элементарного скачка к времени оседлой жизни частицы, отнесенное к одному из шести возможных направлений ее хаотического блуждания. Если S выразить в сантиметрах, а t – в секундах, то размерность D – см²/с. Таким образом, D показывает, как быстро со временем смещаются хаотически блуждающие частицы.

Коэффициент хаотической самодиффузии можно определить как величину, характеризующую способность атомов данного вещества к взаимному перемешиванию при отсутствии в кристалле каких-либо градиентов.

Величина n/t определяется несколькими факторами. Прежде всего, она зависит от того, как долго частице приходится ждать очередной флуктуации (времени оседлой жизни). Это время связано с общим уровнем беспорядка в кристалле: чем выше этот уровень, тем меньше t, т.е. больше n/t (чем выше уровень беспорядка в кристалле, тем менее прочны связи между атомами). Таким образом, этот фактор, имея, в сущности, ту же природу, что и тепловое разупорядочение в кристалле, должны быть экспоненциальной функцией температуры. Кроме того, он должен зависеть от «обычной» (дебаевской) частоты колебаний частицы, равновесной для данных условий, а также энергии, необходимой для преодоления частицей потенциального барьера

,

где w – характеризует вклад в частоту перескоков за счет тепловых флуктуаций, n – частота колебаний частицы при данных равновесных условиях, DG_n – энергия активации диффузии, представляющая собой изменение свободной энергии Гиббса при переходе частицы из равновесного в активированное состояние

где DH_n – высота потенциального барьера.

Однако, для того, чтобы произошел элементарный акт диффузии, необходимо наличие вблизи узла вакансии (при вакансионном механизме) или вакантного междоузлия (при межузельном механизме диффузии). С другой стороны, вероятность занятия вакансией или междоузлий соседними частицами зависит от числа таких соседей: чем их больше, тем больше вероятность обмена местами – после того, как какая-нибудь из них в результате тепловой флуктуации получит запас энергии, достаточной для перескока.

где X – концентрация вакансий для незанятых междоузлий, Z – число соседних узлов, занятых частицами или число соседних междоузлий.

Если концентрацию незанятых междоузлий выразить в молярных долях, то можно принять Х = 1. Тогда для междоузельного механизма переноса имеем

.

При вакансионном механизме диффузии концентрация вакансий составляет величину порядка 10^-5 – 10^-4 (не выше). Т.е., если при переходе от одного механизма к другому Z и w не слишком сильно меняют свои значения, то оказывается, что

Это приводит к существенному различию коэффициентов диффузии для различных механизмов переноса. Таким образом, можно ожидать, что при прочих равных условиях D_i >> D_V.

Если длину элементарного скачка в кубической решетке выразить через ее параметр, то

D= a a² Xw, (7.1)

где коэффициент a (геометрический фактор) учитывает различие между длиной скачка и периодом решетки.

Для междоузельного механизма переноса Х = 1 и имеет место соотношение D = a a²w.

Поиск по сайту: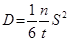