 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Направленная диффузия. Законы Фика
Диффузия, обусловленная градиентом концентрации, считается направленной. Различия коэффициентов самодиффузии означают, что интенсивность хаотических перемещений в кристалле может быть различной. Несмотря на это, распределение дефектов в равновесном кристалле окажется статистически равномерным до тех пор, пока концентрационные, электрические или тепловые поля так же будут оставаться равномерными, или, что, то же самое, градиенты этих полей будут равны нулю. Для равновесных кристаллов это условие является обязательным. Пусть нам удалось в одной из двух соседних кристаллографических плоскостей кристалла простого вещества часть атомов удалить из своих узлов, в результате чего концентрация вакансий в плоскости 1 окажется выше, чем в плоскости 2(CV(1) > CV(2)). Это приведет к возникновению градиента концентрации, вследствие чего часть атомов с плоскости 2 переместится на плоскость 1. Каждый при этом совершает путь S, равный расстоянию между плоскостями. В результате концентрация вакансий в плоскости 2 окажется выше, чем в следующей за ней плоскости 3 и т.д. Переход частицы через объем кристалла, заключенный между плоскостями 1-ой и Р-ой должен осуществляться минимум (Р – 1) скачками. Если считать, что частица перемещается перпендикулярно к кристаллографическим плоскостям, то общий путь, пройденный частицей Dх = S(P – 1). Перепад концентраций вакансий вдоль этого пути составит
Наряду с потоком реальных частиц существует поток вакансий в обратном направлении. Если представить этот поток через некоторое сечение W в течение бесконечно малого времени dt в направлении координаты х, то он должен быть пропорционален градиенту концентрации вакансий вдоль этой координаты:
или
где jV – плотность потока. Уравнение (7.10) сохраняет свой вид и при описании направленной диффузии реальных частиц; вместо градиента концентрации вакансий в него войдет градиент концентрации реальных частиц. В литературе равенство (7.10) известно как закон Фика. В этом уравнении физический смысл коэффициента D следующий: при gradC = 1, dt = 1, W = 1, dnV = D, то есть коэффициент D показывает, какое число частиц или квазичастиц проходит в единицу времени через единичное сечение поверхности при градиенте концентрации равном единице. Определим, какими факторами определяется величина коэффициента диффузии. Частота ухода частиц из своих мест определяется, прежде всего, частотным фактором w. Но абсолютная величина w несколько другая, чем для хаотической самодиффузии, так как под действием сил, обеспечивающих направленный перенос, энергия активации перескока частиц из одного положения в другое несколько изменится. Если мы хотим оценить уход частиц с какой-либо плоскости, то должны учесть, что плотность потока частиц является функцией плотности частиц, приходящихся на единицу поверхности (поверхностной концентрации). Если рассматривать перескок частиц в направлении, перпендикулярном выбранной плоскости, то при отсутствии градиента концентрации такой поток в обе стороны равновероятен. При отсутствии градиента концентрации плотность потока частиц в любой плоскости в одну сторону может быть записан как j = 1/2wCS. Пусть С1 < C2, тогда
В этом случае поток частиц из плоскости 2 в плоскость 1 окажется выше обратного потока. Результирующий поток между плоскостями 1 и 2 запишем в виде
Сравнивая (7.10) и (7.11) получим, что коэффициент направленной диффузии
Вспомним, что
Если перемещение частиц является направленным, то для того, чтобы сделать условия сопоставления равнозначными, учитывать окружение движущейся частицы не следует (z = 1). Пусть мы имеем дело с междоузельным механизмом диффузии. Тогда Х = 1 и Dхаотич=1/6wS2. Таким образом, две формулы качественно одинаковы. Однако, так как наложение поля изменяет величину энергии активации диффузии, это должно внести свой вклад в количественное различие между Dхаотич и Dнапр. Выделим на пути продвижения вакансий в кристалле слой протяженностью dx и сечением W, то есть объемом dV = W.dx. Число вакансий, оседающих в этом объеме за время dt можно выразить как производную концентрации вакансий по времени, умноженную на объем слоя и интервал времени:
Вместе с тем это число будет представлять собой разность между числом вакансий, входящих в указанный слой и выходящих из него:
Сравнивая (7.12) и (7.13), получаем
Это уравнение – математическое выражение 2-го закона Фика. Оно верно для нестационарных потоков, когда концентрация меняется во времени. Для описания переноса во всех трех направлениях уравнение (7.14) используется в виде:
Поиск по сайту: |

 (7.10)
(7.10)

 (7.11)
(7.11)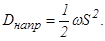

 (7.12)
(7.12) ;
; ;
; ;
; (7.13)
(7.13)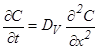 . (7.14)
. (7.14)