|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Электрическая проводимость
Уравнение Нернста–Эйнштейна
Под электрической проводимостью подразумевают способность вещества переносить электрические заряды. Эта способность определяется концентрацией носителей заряда и их подвижностью
s = q.c.u. Скорость V направленного движения заряженных частиц или квазичастиц под действием электрического поля является функцией напряженности поля
V= u.E,
где Е – напряженность поля, u –коэффициент пропорциональности, названный подвижностью. Подвижность – скорость дрейфа носителей заряда в поле единичной напряженности. Между коэффициентом диффузии D заряженных частиц и их подвижностью u существует связь. Пусть кристаллографические плоскости 1, 2, 3 (рис. 7.3) заселены ионами одного сорта. При отсутствии градиента уход ионов с каждой плоскости сбалансирован приходом их с других плоскостей, причем односторонний поток с каждой из них описывается соотношением j = 1/2c.w.s. Когда кристалл оказывается под воздействием электрического поля, указанный баланс обмена ионами между соседними плоскостями нарушается: в соответствии с вектором градиента общий поток ионов в одном направлении растет, а в другом уменьшается.
Рис. 7.3
Тогда
где f – множитель, характеризующий указанные факторы. Пусть градиент поля направлен от плоскости 3 к плоскости 1. Тогда вероятность перескока ионов с плоскости 2 на плоскость 3 уменьшится. Это обусловлено тем, что при каждом скачке, кроме преодоления обычного потенциального барьера, иону требуется дополнительная энергия, чтобы преодолеть силы поля F на расстоянии элементарного скачка, равном расстоянию между соседними плоскостями (S). Чем больше сила поля и чем больше расстояние между плоскостями, тем больше должна быть эта дополнительная энергия. Влияние тормозящего действия поля на частоту перескока (в направлении, обратном направлению градиента поля) связано с температурой, поскольку с повышением температуры частота ухода частиц из своих узлов экспоненциально возрастает. Учитывая перечисленные факторы, можно записать, что в отрицательном направлении (против поля) частота перескоков уменьшится в Поток ионов в направлении поля
а в обратном направлении
Результирующий поток окажется равным:
При условии, что Fs << 2kT
тогда
Учитывая, что коэффициент направленной диффузии
Сила поля характеризуется его напряженностью E и зарядом ионов q:
где Z – валентность иона, е – заряд электрона. Тогда
С другой стороны, результирующий поток ионов можно выразить как произведение их концентрации на скорость движения
что в конечном итоге дает
Это уравнение, устанавливающее связь между подвижностью и коэффициентом диффузии, называется уравнением Нернста – Эйнштейна.
Поиск по сайту: |
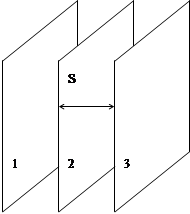

 раз, а в положительном, где энергия требующаяся для перескока, окажется меньше энергии «обычного» потенциального барьера, увеличивается во столько же раз.
раз, а в положительном, где энергия требующаяся для перескока, окажется меньше энергии «обычного» потенциального барьера, увеличивается во столько же раз.

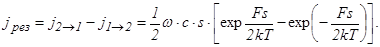
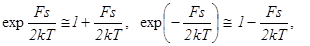
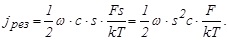
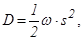 получим
получим
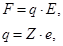

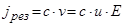 ,
,