|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Статическая ВАХ арсенида галлия
Получим зависимость скорости дрейфа электронов от поля υД(E) для случая отрицательного дифференциального сопротивления. Продифференцировав уравнение
Тогда условие существования отрицательной дифференциальной проводимости можно записать в виде:
Предположим, что распределение электронов между долинами выражается следующим образом:
где k – константа; Обозначим также отношение подвижностей в нижнем и верхнем минимумах как константу:
Предположим, что подвижности μ1 и μ2 не зависят от поля и что локальное распределение электронов между минимумами мгновенно следует за изменениями поля как во времени, так и в пространстве. В арсениде галлия, в котором междолинные переходы электронов определяются процессами рассеяния на оптических фононах, эффективное время рассеяния имеет величину 10-12 сек. Следовательно, для рабочих частот примерно 10 ГГц или ниже междолинные переходы можно считать мгновенными [34, 20]. Для концентрации n1 и n2 можно записать:
где Средняя скорость при данной напряженности поля равна:
На рисунке 8.4 приведена зависимость дрейфовой скорости в зависимости от напряженности электрического поля, рассчитанная по соотношению (8.7) для арсенида галлия.
Рис. 8.4. Зависимость скорости дрейфа от напряженности поля для GaAs Пороговая напряженность поля EП, при которой начинается участок ОДС, по экспериментальным данным равна ~3,2 кВ/см. Значение подвижности при низких полях равно ~8000 см2/В·с, начальное значение дифференциальной отрицательной подвижности ~2400 см2/В·с. Напряженность поля, при которой кончается участок ОДС, приблизительно равна 20 кВ/см.
Электронные температуры (Te) в обеих долинах будем считать одинаковыми. Тогда, пользуясь статистикой Максвелла – Больцмана, запишем:
где m1*, m2* – эффективные массы в долинах, n1, n2 – концентрации электронов в долинах, M2 – число верхних долин, M1 – число нижних долин. {GaAs: M1= 1, M2= 4, m1* = 0,067m0, m2* = 0,55m0, Теперь имеем:
Получим выражение для электронной температуры. Воспользуемся условием баланса энергии, приобретаемой электронами в электрическом поле в единицу времени и теряемой в это же время за счет столкновений с фононами [32]:
τe – время релаксации энергии (~10-12 с).
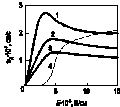
На рисунке 8.5 приведена расчетная зависимость дрейфовой скорости электронов в GaAs при различных температурах, иллюстрирующая влияние температурной зависимости подвижности в обоих минимумах.
Рис. 8.5. Зависимость дрейфовой скорости электронов в GaAs от E при T, K [32, 35]: 1 – 200, 2 – 300, 3 – 350. Кривая 4 – заселенность верхней долины при 300 К
Поиск по сайту: |
 по напряженности электрического поля, получим:
по напряженности электрического поля, получим: .(8.2)
.(8.2)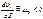 .(8.3)
.(8.3) ,(8.4)
,(8.4)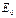 – напряженность поля, при которой
– напряженность поля, при которой 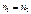 .
. .(8.5)
.(8.5) ;(8.6)
;(8.6)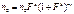 ,
, .
. .(8.7)
.(8.7)
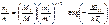 ,(8.8)
,(8.8) }.
}.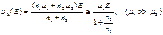 ;(8.9)
;(8.9) .(8.10)
.(8.10) , (8.11)
, (8.11) .(8.12)
.(8.12)