 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Проверочный расчёт вала ⇐ ПредыдущаяСтр 7 из 7
3.1. Исходя из найденных длин отдельных участков вала находим места приложения сосредоточенных внешних нагрузок Fr, Ft, Ft1 Ft2, перенеся их в центры тяжести сечений С (колесо) и D («звёздочка»), т.е. значения длин участков AC, CD, DB (рис. 1):
Рис.1.Силы на валу
AC=
CD=
DB = AC =
На примере схемы нагружения № 5 (при другой схеме нагружения - внести поправки в рис. I и в дальнейшие расчеты и рисунки) строим эпюры 3.2. Определение сил реакций опор в вертикальной плоскости:
Проверка:
3.3. Расчет внутренних изгибающих моментов по длине вала в вертикальной плоскости МB- и построение эпюры этих моментов – ЭМВ(рис. 2):
3.4. Определение сил реакций опор в горизонтальной плоскости:
_______________________________________
_______________________________________
Проверка:
3.5. Расчет внутренних изгибающих моментов в горизонтальной плоскости Мг и построение эпюры этих моментов – ЭМг (см. рис. 2);
Рис. 2. Построение эпюр моментов для схемы нагружения №5.
3.6. Расчет суммарных (полных) изгибающих моментов МΣ
3.7. Построение эпюры крутящих моментов Т (см. рис. 2):
3.8. Расчет эквивалентных моментов no IV теории прочности и построение эпюры приведённых (эквивалентных) моментов – Мэкв (см.рис.2):
3.9. Уточненный диаметр вала d2 с учетом крутящих и изгибающих моментов:
где σ-1 =_______ МПа - предел выносливости для заданного материала из прил. 4. Полученное значение диаметра d2 округляется в большую сторону (прил. 1). Большее из двух найденных диаметров валаd2 (см. п, 2.6) берем за основу: d2 =______мм. 3.10. Моменты сопротивления НЕТТО в опасном сечении II-II (где Mэкв принимает максимальное значение из эпюры на рис. 2): - осевой момент сопротивления
= ______ мм3; - полярный момент сопротивления
= ______ мм3;
где d2 – диаметр вала в опасном сечении II-II в мм; t1 = _______, мм – глубина шпоночного паза вала; b = ______, мм - посадочная ширина шпоночного паза. 3.11. Максимальные напряжения в опасном сечении II-II: -нормальные напряжения от изгиба σmax, МПа:
-касательные напряжения от кручения
3.12. Проверка статической прочности:
где σy из прил. 4. 4. Уточненный расчет вала Необходимо рассмотреть опасное сечение II-II. Найдём общий коэффициент безопасности n в этом сечении и сравним
Для сечения II—II: σm= 0, σα= σmax = __________МПа;
где nσ - запас прочности по изгибу (при отсутствии кручения); σа и τа - амплитуды напряжений цикла;
Κσ. Κτ - эффективные коэффициенты концентрации напряжений для канавки (табл. 3 прил. 5) или галтели (табл. 2 прил. 5);
ψσ; ψτ - коэффициенты, характеризующие чувствительность материала вала к асимметрии цикла переменных нормальных и касательных напряжений (см. прил. 4); β - коэффициент качества поверхности, учитывающий поверхностное состояние вала (прил. 7). Следовательно, условие прочности по усталостному разрушению выполняется.
Поиск по сайту: |

 = ______ мм;
= ______ мм; = ______мм;
= ______мм; = ______мм.
= ______мм. .
.

 _______ H.
_______ H.

 ________H.
________H.
 Н∙м;
Н∙м; ________ Н∙м;
________ Н∙м; ________ Н∙м;
________ Н∙м; _________ Н∙м;
_________ Н∙м; _______ Н∙м;
_______ Н∙м; _______ Н∙м.
_______ Н∙м.
 _________ H.
_________ H.
 _______H.
_______H.
 _______ Н∙м;
_______ Н∙м; _______ Н∙м;
_______ Н∙м; ________Н∙м;
________Н∙м; _____________ = _______Н∙м;
_____________ = _______Н∙м; ___________Н∙м;
___________Н∙м; ________ Н∙м.
________ Н∙м.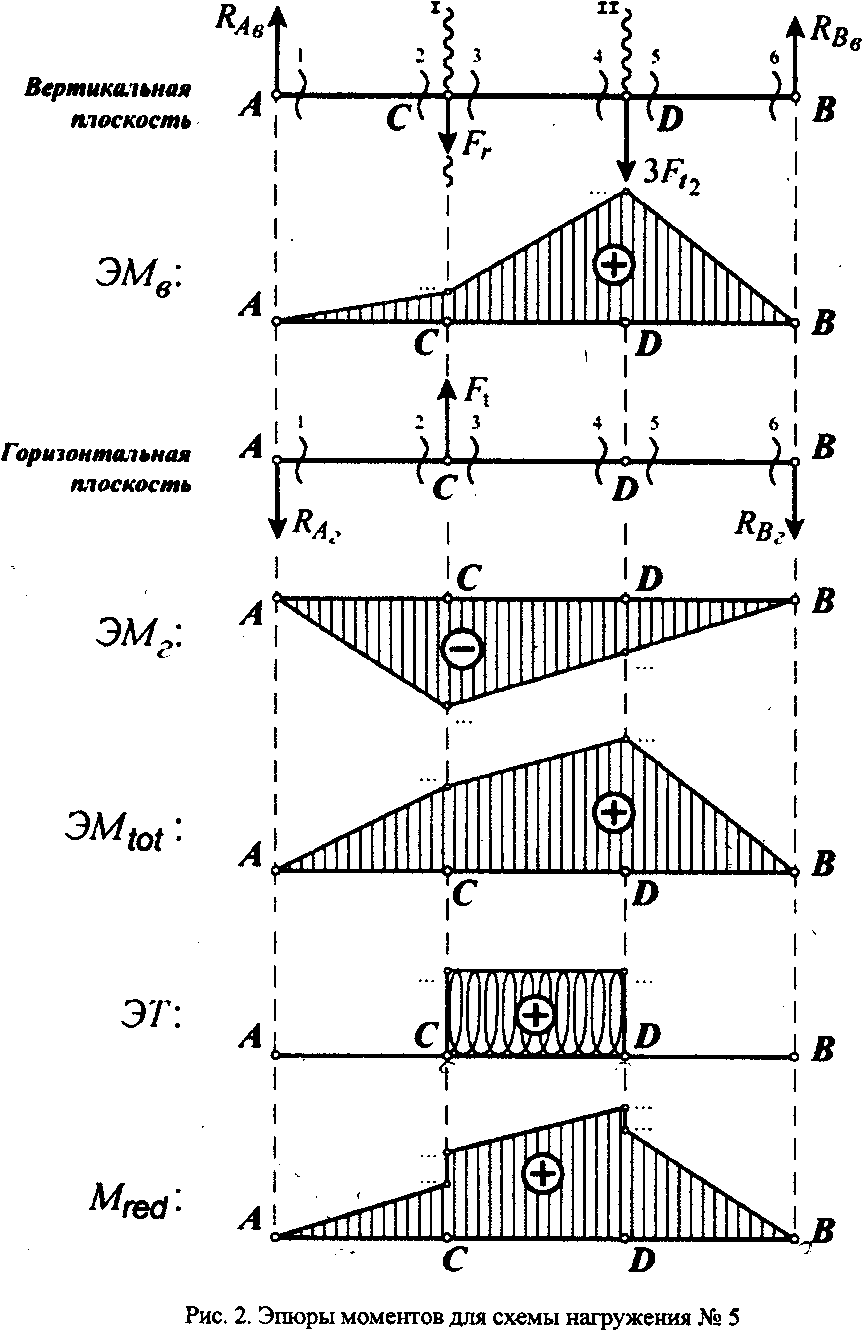
 ________ Н∙м;
________ Н∙м; ______________________ = _________ Н∙м;
______________________ = _________ Н∙м; ___________ Н∙м;
___________ Н∙м; ______________________ = __________Н∙м;
______________________ = __________Н∙м; ___________ Н∙м;
___________ Н∙м;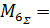 __________ Н∙м.
__________ Н∙м. __________ Н∙м;
__________ Н∙м; __________ Н∙м;
__________ Н∙м; __________ Н∙м;
__________ Н∙м; __________ Н∙м;
__________ Н∙м; __________ Н∙м;
__________ Н∙м; __________ Н∙м;
__________ Н∙м; _____________ Н∙м;
_____________ Н∙м; _____________ Н∙м;
_____________ Н∙м; _____________ Н∙м;
_____________ Н∙м; _____________ Н∙м;
_____________ Н∙м; _____________ Н∙м;
_____________ Н∙м; _____________ Н∙м;
_____________ Н∙м;
 - максимальное значение эквивалентного момента из эпюры Mэкв, Н∙м;
- максимальное значение эквивалентного момента из эпюры Mэкв, Н∙м; , мм3:
, мм3:
 , мм3
, мм3
 = ______ МПа;
= ______ МПа;
 = ______ МПа.
= ______ МПа. = _______ МПа,
= _______ МПа,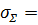 _____ ≤ [σ] ≈ 0,8∙σy = 0,8∙____ = ______ МПа,
_____ ≤ [σ] ≈ 0,8∙σy = 0,8∙____ = ______ МПа, = 2,0, т.е. определим выполняется
= 2,0, т.е. определим выполняется = 2,0 :
= 2,0 :






 и
и  динамические коэффициенты;
динамические коэффициенты; ;
;  - масштабные коэффициенты, учитывающие величину
- масштабные коэффициенты, учитывающие величину