 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Последовательность проверочного расчета вала
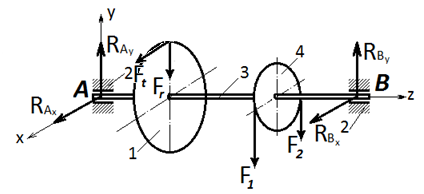
При переходе от конструкции вала к расчетной схеме производят схематизацию нагрузок. Расчет базируется на разделах сопротивления материалов, где рассматривается сложно-напряженное состояние при переменных нагрузках. 1. В схеме нагружения вала (см рис. 3.1) отбрасываем опоры-подшипники и заменяем их силами реакций опор, RAв, RBв - в вертикальной плоскости;RAг, RBг в горизонтальной плоскостирис. 3.4.
Рис. 1.4. Схема нагружения вала
Проектируем все внешние силы, действующие на вал, сначала на вертикальную плоскость хAz , а затем на горизонтальную хАу . Строим расчетные схемы вала для усилий, действующих в вертикальной и горизонтальной плоскостях: ¾ в вертикальной плоскости, силы реакций опор RAв, RBв; радиальное усилие Fr и натяжение ведущей и ведомой ветвей «звездочки» цепной передачи – F1, F2 (в данном случае нагружения вала - рис. 3.5);
Рис. 3.5. Расчетная схема нагружения вата в вертикальной плоскости
¾ в горизонтальной плоскости, силы реакций опор;RAг, RBг и окружное усилие Ft - рис. 3.6:
2. Используя уравнения равновесия статики твердого тела, определяем опорные реакции в местах установки подшипников в вертикальной и горизонтальной плоскостях. Для этого составляем уравнения суммы изгибающих моментов в вертикальной плоскости относительно подшипника А, а затем относительно подшипникаВ: находим силы реакций опор RAв, RBв, выполнив обязательную проверку, чтобы убедиться в том. что реакции определены верно (сумма проекций всех сил на ось y должна быть равна нулю). Затем находим силы реакций опор в горизонтальной плоскости -RAг, RBг и вновь выполняем проверку (сумма проекций всех сил на ось у должна быть равна нулю). Определив силы реакций опор - подшипников в обеих плоскостях, вычисляем внутренние изгибающие моменты по длине вата, пользуясь известным в сопротивлении материалов методом сечений, и строим эпюры этих моментов сначала а вертикальной плоскости, а затем - в горизонтальной (рис. 2 прил. 9). 3. Рассчитываем суммарные (полные) изгибающие моменты МΣ по формуле
и строим под двумя предыдущими эпюрами эпюру суммарных изгибающих моментов MΣ по длине вала (см. рис. 2 прил. 9). 4. Ниже строим эпюру крутящего момента T (см. рис. 2 прил. 9). Величину этого момента T определили ранее в предварительном расчете. 5. Находим приведенные (эквивалентные) моменты Mэкв по четвертой классической гипотезе прочности - энергетической гипотезе формоизменения. (Для пластических материалов наилучшие результаты в смысле совпадения с экспериментами дает четвертая теория прочности - гипотеза Бельтрами - Губер - Мизес - Генки). Под эпюрой T строим по всей длине вала эпюру Мэкв:
6. Уточняем диаметр вала d2 в местах установки зубчатого колеса и «звездочки» с учетом крутящих и изгибающих моментов:
где σ-1 - предел выносливости заданного материала вала (прил. 4) при симметричном цикле нагружения. Найденный диаметр вала d2 округляем в большую ближайшую сторону стандартного значения. Далее за основу должен быть принят больший из двух найденных диаметров d2. 7. Находим моменты сопротивления НЕТТО (с учетом ослабления сечения вала шпоночными пазами) вала изгибу и кручению в самом опасном поперечном сечении по максимальному значению приведенного момента из эпюры Мэкв (сечение II-II). Моменты сопротивления являются геометрическими характеристиками поперечных сечений вала, определяющими прочность вала при изгибе и кручении: - осевой
где d2 - диаметр вала в опасном сечении II-II, мм; t1 - глубина шпоночного паза вала, мм; 8. Определяем максимальные напряжения в сечении II—II: -нормальные от изгиба σmax , МПа:
- касательные от кручения τmax, МПа:
сечении, определяя эквивалентное напряжение σэкв по формуле
где [σ] = 0,8·σy
3.5. Уточненный расчет вала Практикой установлено, что для валов основным видом разрушения является усталостное, поэтому расчет валов на сопротивление усталости служит основным. Главным критерием для вывода об опасности сложнонапряжённого состояния является запас прочности по сопротивлению усталости (выносливости) материалаn. Оценку прочности выполняют в форме расчета запаса прочности n при переменных напряжениях по усталостному разрушению в опасном сечении и путем сравнения его с допускаемым (нормативным) nн, т.е. при выполнении условия усталостной прочности: n ≥ nн. Валы изготавливают из хромоникелевых углеродистых сталей с высоким пределом выносливости. На специальных испытательных машинах, подвергая образцы круговому и симметричному плоскому изгибу (машины Веллера, Шенка), производят испытания на усталость. Целью их является установление предела усталости (выносливости). Эта характеристика получила обозначение по нормальной выносливости при симметричном цикле нагружения σ-1 по касательной – τ-1. Для определения предела касательной выносливости τ-1 может служить формула Людвига: τ-1 = 0,575 σ-1 Приступив к уточненному расчету, выделяем опасное сечение вала, подлежащее проверке: из эпюры эквивалентных моментов Mэкв по максимальному значению определяем самое опасное сечение: II—II. Для рассматриваемой схемы нагружения (пятой) из рис. 2 наглядно видно, что сечение II-II является местом установки «звездочки». Уточненные расчеты отражают влияние на выносливость цикла напряжений, концентрации напряжений, масштабных факторов, состояния поверхности. Валы работают в основном в условиях кручения и изгиба. От скручивающих внешних силовых факторов в поперечных сечениях вала возникают касательные напряжения τ, а от изгибных - нормальные напряжения σ (в общем случае изгиба наличие поперечной силы приводит также к возникновению ещё и касательных напряжений τ, которые определяются по формуле Д.И. Журавского, но они ничтожно малы по сравнению с σ). Коэффициент запаса сопротивления усталости n вычисляют по формуле
Здесь nσ - запас прочности по изгибу (при отсутствии кручения); (3.2)
где σа и τа - амплитуды напряжений цикла:
σm и τm - средние значения напряжений цикла:
Решающую роль при переменных нагрузках на сопротивление усталости играют значения минимального и максимального напряжений цикла и их отношение, т.е. коэффициент асимметрии цикла напряжений R. При расчетах предполагают, что изменение напряжений во времени происходит по закону, близкому к синусоиде. В рассмотренном случае вал испытывает сложное сопротивление, т.к. работает на изгиб с кручением. При таком сложном напряжении принимают, что нормальные напряжения σ, которые возникают в поперечных сечениях вала при изгибе, изменяются по симметричному циклу (рис. 3.7) - наиболее опасному при изгибе, для которого σmax = -σmin ; σа = σ ; σm = 0; R=-1, а касательные напряжения τ, возникающие от кручения, - по отнулевому (пуль- сационному, пульсирующему) циклу (см. рис. 3.7), при котором τmax = τ : τmin = 0; τm = τa = τ/2; R = 0 а). б).
Рис. 3.7. Циклы напряжений при переменных нагрузках: а - симметричный; б - пульсационный (отнулевой)
Выбор пульсирующего цикла для напряжений кручения обоснован тем, что большинство машин работает с переменным крутящим моментом, а знак момента изменяется только у реверсивных машин. Таким образом, для вычисления запаса прочности n в опасном сечении II-II необходимо сначала найти значения σа , σm , τа, τm из ранее приведенных формул (пункт 8, стр. 13):
В формуле (3.2) динамические коэффициенты В формуле (3.2) динамические коэффициенты
При расчете коэффициентов запаса прочности учитывают факторы, Κσ. Κτ - эффективные коэффициенты концентрации напряжений для
ψσ; ψτ - коэффициенты, характеризующие чувствительность материала вала к асимметрии цикла переменных нормальных и касательных напряжений (см. прил. 4); β - коэффициент качества поверхности, учитывающий поверхностное Значения пределов выносливости при симметричном цикле нагружения по нормальным и касательным напряжениям для заданного материала вала σ-1; τ-1 см. в прил. 4. Найдя по формуле (3.1) величину n для самого опасного сечения вала
т.е. необходимо, чтобы выполнялось условие: n ≥ [nн] = 2,0. Если окажется, что общий расчетный коэффициент запаса прочности
Поиск по сайту: |





 - максимальное значение эквивалентного момента из эпюры, Мэкв
- максимальное значение эквивалентного момента из эпюры, Мэкв  , мм3:
, мм3: - полярный
- полярный 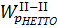 , мм3:
, мм3:

 .
.







 и
и  определяются следующим образом:
определяются следующим образом:
 ;
;  - масштабные коэффициенты, учитывающие величину
- масштабные коэффициенты, учитывающие величину