 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Поражающее действие волны прорыва.
В целом ряде случаев при оценке состояния зданий, сооружений в зоне затопления, необходимо знать ущерб, нанесенный этим сооружениям. Для оценки ущерба в приближенных расчетах используются данные табл.11. Более строгие оценки могут быть получены при сопоставлении величины ущерба с вероятностью поражения сооружения. Вероятность поражения в этом случае является математическим ожиданием ущерба. Необходимо отметить, что в табл.24 критерии безусловного поражения (полного разрушения) и безопасности зданий отсутствуют. В приближенных расчетах при отсутствии указанных данных за значение параметра определяющего нижнюю границу безусловного поражения сооружения, допустимо принять (с определенными оговорками) верхнее значение Пример.Определить вероятность поражения волной прорыва промышлен ного здания с легким металлическим каркасом, расположенного на берегу реки в зоне затопления. Высота потока у здания 4 м , скорость течения 2,5 м/с. Решение.1. Так как критерии безусловного поражения и безопасности рассматриваемого здания в табл.24 отсутствуют, примем за первый из них – верхнее значение
2. По формулам (2.19) вычисляем значения параметров нормаль- ного закона распределения
4. Вероятность поражения здания находим по первому соотношению (2.17).
Нагонные наводнения. Нагонные наводнения, как правило, наблюдаются при прохождении мощных циклонов.
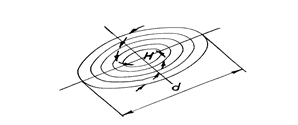
Циклон - это гигантский атмосферный вихрь, рис. 36. Рис. 36. Схема циклона. Н-центр циклона, круговые линии-изобары, стрелки – направление ветра, d - диаметр циклона. Диаметр циклона d =1000 - 2000 км, высота 2 -10 км, давление в центре 950 - 960 мбар (атмосферное давление на уровне моря 1012 мбар), скорость перемещения до 30 - 45 км/час. Воздушные массы в циклоне движутся по спирали, закручивающейся к его центру против часовой стрелки в северном полушарии и по часовой стрелке в южном. Скорость ветра в циклоне может быть до 20 м/с, иногда до 30 м/с. Кинетическая энергия движущихся воздушных масс может достигать величины 4•1017 Дж [11], что соответствует энергии взрыва примерно 100 ядерных зарядов мегатонного класса. Разновидность циклона – тайфун. В переводе с китайского тайфун – очень сильный ветер; в Америке его называют ураганом. Он представляет собой атмосферный вихрь диаметром несколько сотен километров. Давление в центре тайфуна может достигать ~900 мбар. Сильное снижение давления в центре и относительно небольшие размеры приводят к образованию значительного градиента давления в радиальном направлении. Ветер в тайфуне достигает 30¸50 м/с, иногда и более 50 м/с. Тангенциально дующие ветры обычно окружают спокойный участок, называемый глазом тайфуна. Он имеет диаметр 15¸25 км, иногда до ~50¸60 км. По его границе образуется облачная стена, напоминающая стену вертикального кругового колодца. С тайфунами связаны особенно высокие нагонные наводнения [11,12]. При прохождении циклона по морю уровень воды в его центральной части повышается. Высота подъема, называемого барическим, составляет
где Р0 - атмосферное давление на уровне мирового океана, Па; Р - давление в центре цикла, Па; r- плотность воды, кг/м3; g- ускорение свободного падения. В качестве примера определим барический подъём воды, если давление в центре циклона Р = 950 мбар (0,95×105 Па), давление за пределами циклона Р=1012 мбар (1.012×105 Па). По формуле (5.22) вычисляем
Как будто немного, но барический подъем уровня воды происходит на большой площади, измеряемой сотнями и тысячами квадратных километров. При смещении циклона этот подъём воды оседает, растекаясь во все стороны в виде так называемой длинной волны, длина которой в отдельных случаях достигает ~800 км. Будучи незаметной в открытом море, эта волна может стать опасной, когда центр циклона приближается к побережью и волна входит в заливы, бухты. При движении длинной волны по сужающимся заливам и бухтам происходит повышение уровня воды, в несколько раз превышающее начальный барический подъем. В заливах, бухтах аналогично, как в сосудах, жидкая среда имеет определенные величины периодов собственных колебаний. Обладающий большой энергией циклон и порожденная им длинная волна могут возбудить собственные колебания воды (сейши). При этом возможно наложение сейшевых колебаний на длинную волну, приводящее к увеличению (или уменьшению) подъёма уровня воды. В частном случае прямоугольного в плане водоема длиной a, шириной b, глубиной Н0 период сейшевых колебаний определяется по формуле Мериана (при a>b>>H0) [35]
где Т1, T2, Т3 - периоды основного тона и двух обертонов, с; n - номера главных форм колебаний; а - длина водохранилища, м.
Сейшевые колебания – это стоячие волны, рис 37. Рис 37. Сейшевые колебания а – одноузловые, б - двухузловые Например, в Финском заливе наблюдались одно, двух, трёх и четырёхузловые сейши. Амплитуда сейшевых колебаний зависит от энергии возмущающего источника и размеров водоёма. Так в Азовском море наблюдались сейши с амплитудой 10¸25 см и периодом около 23 часов, в Женевском озере – амплитудой до двух метров и периодом более одного часа. Третье обстоятельство, влияющее на величину подъёма уровня воды в заливах, бухтах, связано с ветровым нагоном воды. Когда все перечисленные факторы действуют одновременно, уровень воды поднимается особенно высоко.
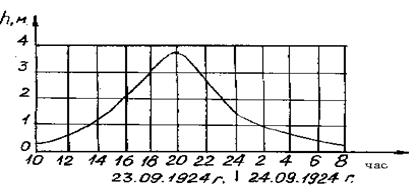
На рис. 8 в качестве примера показано изменение уровня воды в г. Ленинграде при наводнении 23.09.1924 г. [41]. Подъём уровня воды начался в 10 часов утра. Максимальный подъем уровня (3,8 м) наблюдался в 20 часов, после чего начался спад воды.
Рис.38. Изменение уровня воды в Ленинграде На рис. 39. Показано положение поверхности Финского залива в это время.
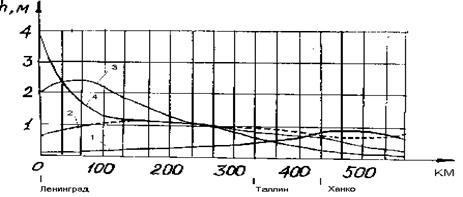
Рис. 39. Профили свободной поверхности Финского залива
На этом рисунке кривая 1 отвечает положению свободной поверхности на время 10 часов, кривая 2-на 13 часов, кривая 3-на 17 часов, кривая 4 -на 20 часов. Видно как по заливу движется длинная волна и как повышается уровень воды в восточной части залива. Волна сгенерирована мощным циклоном, проходящим через Балтийское море. На основании многолетних наблюдений для оценки подъема воды в Ленинграде при нагонном наводнении установлена зависимость [41]
где hЛ - высота подъёма воды в Ленинграде; hТ - высота волны в районе Таллинна; Значения
где Таблица 25
Поиск по сайту: |
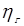 , м
, м
 ,м/c
,м/c
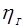 , м
, м
 , м
, м
 , м/с
, м/с
 , при котором имеют место сильные разрушения. Одновременно за значение параметра, определяющего границу безопасности, допустимо принять нижнее значение
, при котором имеют место сильные разрушения. Одновременно за значение параметра, определяющего границу безопасности, допустимо принять нижнее значение 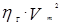 , при котором имеют место слабые разрушения. Последующий расчет вероятности поражения сооружения проводится по формулам (2.15) – (2.19).
, при котором имеют место слабые разрушения. Последующий расчет вероятности поражения сооружения проводится по формулам (2.15) – (2.19). , отвечающее сильным разрушениям здания, за второй – нижнее значение
, отвечающее сильным разрушениям здания, за второй – нижнее значение  ;
;
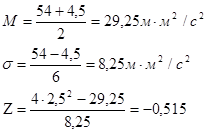
 3. По третьему соотношению (2.17) вычисляем значение функции
3. По третьему соотношению (2.17) вычисляем значение функции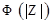 .
.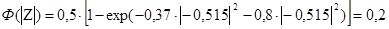
 .
.
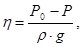 (5.22)
(5.22)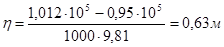 .
.
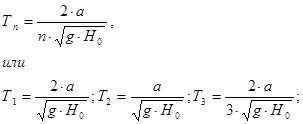 (5.23)
(5.23)
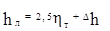 , (5.24)
, (5.24)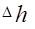 - дополнительный подъем уровня воды, связанный с ветровым нагоном воды.
- дополнительный подъем уровня воды, связанный с ветровым нагоном воды.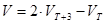 , (5.25)
, (5.25)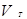 - проекция скорости ветра на ось залива в момент максимального уровня воды в Таллинне;
- проекция скорости ветра на ось залива в момент максимального уровня воды в Таллинне; 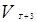 - то же, спустя 3 часа, в районе островов Мощный и Гогланд (расстояние до Ленинграда ~140 км). Связь величин V и
- то же, спустя 3 часа, в районе островов Мощный и Гогланд (расстояние до Ленинграда ~140 км). Связь величин V и