 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Максимальные расходы воды в периоды половодья рек.
Таблица 22 Возможные размеры зон затопления в зависимости от уровня Подъема воды.
Паводок.
Опасность паводкового наводнения состоит в том, что оно может быть неожиданным, например, при прохождении ливневых дождей в ночное время. При паводке имеет место сравнительно кратковременный подъем воды, вызываемый ливневыми дождями или бурным таянием снега. На рис. 32 приведен гидрограф расхода ливневого паводка. Он состоит из восходящего участка, начинающегося в точке А, гребня В и затем нисходящего участка, оканчивающегося в точке С; точку А называют фронтом паводковой волны. Рис. 32. Гидрограф ливневого паводка
На этом рисунке: Td - продолжительность выпадения осадков, Т - продолжительность паводка, Qm - максимальный расход, Q0 - бытовой расход. Паводок относится к нестационарным течениям. При определении параметров водного потока при паводке пользуются системой уравнений Сен-Венана (5.1) (без упрощающих допущений, принимаемых для описания течения жидкости при половодье). Решение системы (5.1) выполняется численно с помощью ЭВМ. Паводок – это волновое движение. Скорость фронта паводка вычисляется по формуле
где Скорость гребня паводка
где Для определения величины h используется формула (5.16), где в данном случае максимальный расход находят по соотношению [34]
где Высота паводка на расстоянии Х от наблюдаемого створа оценивается по соотношению [37]
где С1, C2 - константы, определяемые по наблюдениям высоты паводка в двух створах.
Пример. 0пределить максимальную высоту паводковой волны при выпадении ливневых осадков интенсивностью 40 мм/час на площади 162 км2 в бассейне реки. Русло реки трапецеидальное, ширина русла по дну 100 м, по урезу воды 200 м, глубина реки 4 м, скорость бытового течения 1 м/с. Решение. 1. Находим бытовой расход воды в реке:
2. По формуле (3.19) вычисляем максимальный расход при прохождении паводка
3. По соотношению (5.12) определяем параметр "m" русла реки
4. По формуле (5.16) вычисляем максимальный подъем уровня воды при паводке
§5.4 Волна прорыва при разрушении плотин гидроузлов. Оценка состояния зданий, сооружений в зоне затопления волной прорыва.
При авариях, сопровождающихся разрушением плотины, запасенная потенциальная энергия водохранилища высвобождается в виде волны прорыва (типа мощного паводка), образующейся при изливе воды через проран (брешь) в теле плотины. Волна прорыва распространяется по речной долине на сотни километров и более. Оценим величину запасенной энергии водохранилища на следующем примере. Пусть глубина воды у плотины в верхнем бьефе Н0= 55 м, в нижнем бьефе h0=5м, длина плотины В=5000 м, длина водохранилища L= 40.000 м, рис. 34.
1 – плотина, 2 – водохранилище. Потенциальная энергия водохранилища может быть найдена по соотношению
Здесь Для сравнения энергия ядерного взрыва мощностью q = 106 т (в тротиловом эквиваленте) составляет Основными параметрами волны прорыва являлся: высота гребня
Рис 35. Волна прорыва. 1 – фронт волны, 2 – гребень, 3 – хвост, H0 - глубина водохранилища, h0 – уровень воды в реке, Для определения параметров волны прорыва решается полная система уравнений Сен- Венана (5.1) по машинным программам, разработанным в Сибирском отделении АН РФ и институте “Гидропроект” им. С. Я. Жука. Некоторые результаты полученного решения приведены, например, в [14,37 – 40]. В качестве примера в табл. 4 и 5 приведены данные по величинам Таблица 23.
Поиск по сайту: |
, м
, (5.17)
- скорость и глубина основного потока соответственно; 
- коэффициент, зависящий от формы русла (для реальных русел приближенно принимают a »0,8).
, (5.18)
- подъем уровня воды при прохождении паводка.
(5.19)
- максимальный расход, м3/с; 
- расход до выпадения осадков, м3/с; 
- интенсивность осадков, мм/час;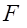 
- площадь района выпадения осадков в бассейне реки, км2; 
- коэффициент, учитывающий долю стока осадков в реку (обычно 0<k£1, в приближенных расчетах для оценки максимально возможного паводка допускается принимать k»1).
, (5.20)
м3/с.
м3/с.
м.
- плотность воды, кг/м3, g = 9,81 м/с2 – ускорение свободного падения.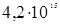
Дж.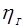
, наибольшая скорость течения Vm, время прихода фронта tФ, гребня tГ, хвоста tX. На рис. 35 показано продольное сечение волны прорыва.
- высота гребня волны.
при распространении волны прорыва по схематизированному прямоугольному руслу для трех характерных гидроузлов равнинного и предгорного типов при ширине прорана Bпр 
0.5 В, где В – длина плотины. Это случай, близкий к полному разрушению плотины. Более полные данные по параметрам волны прорыва при различных значениях, Bпр, 
изложены в литературе [37,38].