 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Устойчивость этого массива определяется величиной коэффициента
При c > 1 массив устойчив; при c < 1 массив обрушится. Коэффициент c называется коэффициентом устойчивости. В практике проведения различных инженерных и строительных работ нередко требуется установить предельную высоту склона, при которой он сохраняет устойчивость, и положение возможной поверхности скольжения при потере устойчивости. Вес массива АВС (принимая его толщину равной единице измерения) составляет
где r - плотность грунта; g - ускорение свободного падения. Положение возможной поверхности скольжения наиболее опасно, так как для обеспечения равновесия необходимо обеспечить максимальное сцепление “С” (на других поверхностях равновесие обеспечивается при меньших значениях “С”). Решая уравнения (3.2) и (3.4) относительно “С” и принимая
Подставляя данное соотношение в уравнение (3.2) и решая его относительно H, можно найти критическую высоту Нкр, при которой сохраняется устойчивость склона [11]
где y(a,j) - играет роль коэффициента устойчивости. Значения коэффициента y(a,j) приведены на рисунке 21а; при j=0 (водонасыщенные глины) y(a,j) = В случае, если поверхность скольжения имеет круглоцилиндрическую форму, рис. 20, критическая высота откоса Нкр находится по соотношению [11] Нкр= где значения коэффициента y(a,b,j) снимаются с графиков рис. 21б.
Рис.21. Значения коэффициента y для моделей обрушения откосов с плоской а) и круглоцилиндрической б) поверхностями скольжения.
Положение поверхности скольжения находится методом последовательных приближений. Определяется такое положение этой поверхности (задаются положение центра вращения “О” и величина радиуса “r”), при котором для поддержания равновесия рассматриваемого массива требуется наибольшая величина сцепления. По условию равновесия сумма моментов всех сил относительно центра вращения должна равняться нулю. Например, при j = 0 условие равновесия применительно к схеме рис. 20 может быть представлено в виде
Коэффициент устойчивости склона
Склон теряет устойчивость при c < 1 . Следует отметить, что землетрясение может спровоцировать обрушение склона. Как отмечалось ранее в §1.7, при землетрясении имеют место горизонтальные и вертикальные ускорения грунта, обусловленные продольной, поперечной и поверхностной сейсмическими волнами. Для получения представления о механизме воздействия землетрясений рассмотрим случай воздействия горизонтальных ускорений, имеющий место при распространении продольной волны. Согласно принципу Д’Аламбера, воздействие ускорения
При оценке устойчивости склонов, сложенных скальными породами следует иметь в виду, что потенциальные поверхности скольжения чаще всего имеют форму, предопределённую наиболее распространёнными системами трещин. При этом сцепление по поверхностям трещин может быть близким к нулю. Пусть смещение части скального откоса происходит по ранее образованным трещинам (или трещине), рис. 22.
Рис. 22. Склон, пересекаемый трещиной.
Условие скольжения блока АВС можно записать в виде
где Р – вес блока; j ¢ - угол трения по трещине. Коэффициент устойчивости блока АВС c*=
Оползни. Оползни – это смещение на более низкий уровень части горных пород, слагающих склон, в виде скользящего движения в основном без потери контакта между движущимися и неподвижными породами. Движение оползня начинается вследствие нарушения равновесия склона и продолжается до достижения нового состояния равновесия. Перемещение значительной массы породы, вызванное оползнем, может привести к тяжёлым последствиям. Оползни могут разрушить различные объекты, а в некоторых случаях и населённые пункты, погубить сельскохозяйственные угодья, повредить коммуникации, туннели, телефонные и электрические сети, угрожать водохозяйственным сооружениям (плотинам). Основные причины образования оползней [14]: чрезмерная крутизна склона (откоса); перегрузка верхней части склона инженерными сооружениями; нарушение целостности пород склона оврагами, траншеями; подрезка склона у его подошвы; увлажнение подошвы склона; смачивание плоскостей напластования (контактов) подземными водами в результате обильных дождевых осадков и бурного таяния снега. Движение оползня начинается с момента, когда коэффициент устойчивости склона, определяемый согласно рекомендациям предыдущего параграфа, становится меньше единицы. Для получения представления о последующем движении оползня рассмотрим два важных частных случая: когда его тело сложено из глинистых пород и из скальных пород. В первом случае сопротивление движению оползня обычно определяют сцеплением “C” (угол внутреннего трения глин j » 0). Энергетический баланс массы ”m”, смещающейся вниз по склону под углом b, рис. 23, может быть представлен в виде
где mg - вес оползня; DH - его вертикальное смещение; L - площадь контакта оползня; CL - сила сцепления;
v – скорость оползня. Принимая ширину оползня, равной единице измерения, его можно представить в виде
Видно, что при b = const возникающий оползень продолжает смещаться с нарастающей скоростью (при изменении величины DH от 0 до Н).
Рис. 23. Схема оползня.
Во втором случае сопротивление движению оползня определяется не сцеплением, а коэффициентом сухого трения f . Энергетический баланс массы оползня, смещающейся по склону, запишется в виде
где используются те же обозначения, что и в соотношениях (3.13) и (3.14). Принимая, что f » tgj , где j - угол внутреннего трения материала оползня (близкий к углу естественного откоса), можно получить
Видно, что образовавшийся оползень смещается вниз по склону также с нарастающей скоростью. Кроме того, смещение из неподвижного состояния произойдёт только при условии Следует отметить, что коэффициент устойчивости склона со временем может меняться. Так при проведении специальных инженерных мероприятий он может увеличиться, но обычно в результате негативных природных явлений и ошибок хозяйственной деятельности человека он уменьшается. Учёт таких воздействий проводится введением в коэффициент устойчивости определённых поправок [14]. Для определения поправок рассчитывают среднее годовое уменьшение коэффициента устойчивости за год Dc. Находят зависимость амплитуды обратимых колебаний коэффициента устойчивости от негативных воздействий и вычисляют среднюю величину амплитуды его отрицательного отклонения Dcср и максимальную её величину Dcmaxза период времени T. Определяют возможность оползня в конце периода Т по соотношению
где c - коэффициент устойчивости склона в конце периода Т; c0- начальное значение коэффициента устойчивости. Если если если Вероятное время возникновения оползня Т*оценивают по соотношению
Пример: Определить вероятное время возникновения оползня. Начальное значение коэффициента устойчивости склона Решение: Время вероятного смещения оползня вычисляем по соотношению (3.18):
то есть через 34…48 лет.
Обвалы. Горные удары. Обвалы происходят на крутых скальных уступах. Может произойти обвал одной глыбы или целого массива. Десятки тысяч тонн породы при потере устойчивости могут внезапно отделиться и рухнуть вниз. Возможность обвала определяется по соотношению (3.17), где под величиной c0в этом случае подразумевается значение c*из (3.12). Во время движения скорость обвала возрастает. Из соотношения (3.16) следует, что для крутых склонов, когда угол Горным ударом называется внезапное, очень быстрое разрушение некоторой части скального массива, происходящее в виде откола (в технической литературе используется термин “отстрел”). При этом по скальному массиву распространяется система упругих волн (типа волн, описанных в параграфе 1.11), воспринимаемых как удар или серия ударов. На рис. 24 схематично изображён подработанный вертикальный откос, разрушение которого может привести к горному удару. Пунктирная линия на этом рисунке соответствует поверхности максимальных растягивающих напряжений, нормальных к поверхности вертикального откоса. Если растягивающие напряжения превзойдут предел прочности скального грунта на разрыв, произойдёт откол.
Механизм горных ударов связан с внезапным высвобождением накопленной упругой энергии при отколе ослабленной части скального массива. Потенциальная энергия деформаций рассматривалась ранее в параграфе 1.6. Высвобождаемая энергия определяет масштаб последствий горных ударов.
§ 3.5. Скатывающиеся камни. Оползни, обвалы на откосе из скального грунта, а также сотрясения скального массива при землетрясениях, взрывах и т.п. обычно сопровождаются скатыванием по склону камней (используется термин “камнепад”). При исследовании процесса скатывания камней в приближённых расчётах используется модель камня в форме шара, катящегося вниз по наклонной плоскости, рис. 25.
Пусть v - линейная скорость скатывающегося камня. Кинетическая энергия камня определяется соотношением [32]:
где m - масса камня; J - момент инерции; w - угловая скорость вращения катящегося камня. Известно, что
Тогда
Энергетический баланс камня при его движении от точки А, отвечающей положению покоя, до точки В на рис. 25 можно по аналогии с соотношением (3.15) представить в виде
где f*- коэффициент трения качения. Из выражения (3.22) нетрудно получить:
Согласно [32], трение качения в несколько раз меньше трения скольжения. При известном значении f* расчёт скорости v не встречает затруднений. Видно, что при движении камня по склону его скорость возрастает. Соотношение (3.23) позволяет решить и обратную задачу: определить коэффициент трения качения камня, если известна его скорость движения в конце склона. Разрешая это соотношение относительно f*, нетрудно получить
Довольно часто при движении по склону скатывающихся камней наблюдается явление “подскока”, рис. 24. Подскок происходит, если на пути движения камня встречается невысокое препятствие или имеет место неровность склона. При движении камня по воздушной траектории его скорость v увеличивается быстрее. При большой длине склона подскок может повториться несколько раз. Катящиеся по склону и летящие по воздуху с большой скоростью камни представляют значительную опасность для человека и транспортных средств, движущихся по горным дорогам. Пример: Определить коэффициент трения качения камня, катящегося по склону, если в конце склона у подошвы его скорость составляла 14 м/с. Высота склона 20 м, угол наклона склона 45°. Решение: Коэффициент трения качения находим по соотношению (3.24):
Поиск по сайту: |
 (3.3)
(3.3) , (3.4)
, (3.4) , можно определить наклон поверхности скольжения
, можно определить наклон поверхности скольжения (3.5)
(3.5) , (3.6)
, (3.6) . [11].
. [11]. , (3.7)
, (3.7)
 DL
DL  =0 (3.8)
=0 (3.8) (3.9)
(3.9) на движение массы m равно приложению силы m
на движение массы m равно приложению силы m  к этой массе. Соответственно в расчёте устойчивости нужно добавить силу m
к этой массе. Соответственно в расчёте устойчивости нужно добавить силу m  к другим силам, воздействующим на массу m. Обращаясь к рис. 20, можно выразить коэффициент устойчивости склона в виде (при j = 0)
к другим силам, воздействующим на массу m. Обращаясь к рис. 20, можно выразить коэффициент устойчивости склона в виде (при j = 0) (3.10)
(3.10)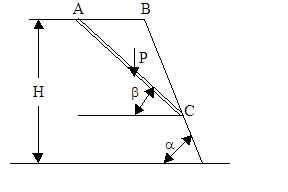
 (3.11)
(3.11) (3.12)
(3.12) , (3.13)
, (3.13) - смещение по склону;
- смещение по склону; , где d - средняя толщина (мощность) оползня, r - плотность материала. Тогда
, где d - средняя толщина (мощность) оползня, r - плотность материала. Тогда (3.14)
(3.14)
 , (3.15)
, (3.15)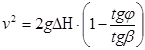 (3.16)
(3.16) или j < b. Оползень прекращает движение на равнине у подножия склона, рис. 23.
или j < b. Оползень прекращает движение на равнине у подножия склона, рис. 23. (3.17)
(3.17) , то оползень маловероятен;
, то оползень маловероятен; , то оползень возможен;
, то оползень возможен; , то вероятность оползня велика.
, то вероятность оползня велика. (3.18)
(3.18) . Среднее годовое уменьшение коэффициента устойчивости вследствие равномерного подмыва подошвы склона
. Среднее годовое уменьшение коэффициента устойчивости вследствие равномерного подмыва подошвы склона  . Среднее годовое отрицательное отклонение коэффициента устойчивости в результате колебаний водонасыщенности склона составляет
. Среднее годовое отрицательное отклонение коэффициента устойчивости в результате колебаний водонасыщенности склона составляет  ; максимальное отрицательное отклонение коэффициента устойчивости за 50 лет
; максимальное отрицательное отклонение коэффициента устойчивости за 50 лет  .
. ,
, , величина
, величина  , при этом
, при этом  . В конце движения, когда величина
. В конце движения, когда величина  становится равной Н, скорость движущегося массива составляет
становится равной Н, скорость движущегося массива составляет  . При такой скорости движущийся грунтовый массив обладает большой разрушительной силой.
. При такой скорости движущийся грунтовый массив обладает большой разрушительной силой.

 , (3.19)
, (3.19)

 , (3.20) где r – радиус шара.
, (3.20) где r – радиус шара. (3.21)
(3.21) , (3.22)
, (3.22) (3.23)
(3.23) , (3.24)
, (3.24)