 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Характеристики координатного закона поражения
3. Строим график координатного закона поражения, рис. 17.
Рис. 17. Координатный закон поражения.
Самостоятельный интерес представляет оценка вероятности дискретной случайной величины. При изучении опасных природных процессов часто бывает необходимым оценить вероятность какого-либо события в течение определенного временного интервала. Вероятность
В этой формуле параметр распределения Пуассона записан в виде Опираясь на соотношение (2.22), нетрудно определить вероятность того, что произойдет ровно одно событие
Вероятность того, что не произойдет ни одного события
а вероятность того, что произойдет хотя бы одно (не менее одного) события
Пример.Пусть в конкретном регионе проходит в среднем три сильных землетрясения за 100 лет ( течение Решение.Вероятность одного сильного землетрясения за период времени вычисляем по формуле (2.23)
Оценка состояния зданий, Сооружений на объекте после землетрясения.
Для оценки состояния зданий, сооружений после землетрясения могут быть использованы данные табл.4. В случаях, когда критерии поражения сооружения не известны, а известно только значение его сейсмостойкости, для определения степени разрушения используется соотношение [23]
где
Значение В целом ряде случаев при оценке состояния зданий, сооружений необходимо также знать ущерб, нанесенный этим сооружениям. Для оценки ущерба в приближенных расчетах используется данные табл.11. [14]
Таблица 11. Величина ущерба в зависимости
Поиск по сайту: |

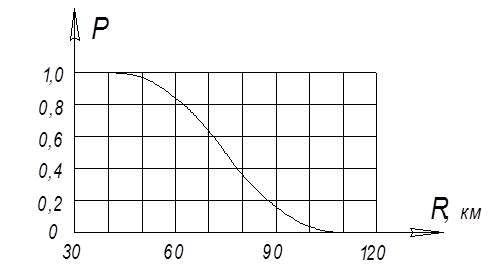
 появления
появления  рассматриваемых событий за период времени
рассматриваемых событий за период времени 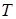 определяется в зависимости от среднего числа
определяется в зависимости от среднего числа  таких событий в единицу времени по формуле (2.20), которая может быть представлена в виде
таких событий в единицу времени по формуле (2.20), которая может быть представлена в виде ,
,  (2.22)
(2.22) .
. (2.23)
(2.23) , (2.24)
, (2.24) (2.25).
(2.25).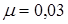 ). Найти вероятность одного такого землетрясения в
). Найти вероятность одного такого землетрясения в лет.
лет. .
. , (2.26)
, (2.26)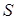 - степень разрушения здания (
- степень разрушения здания (  см § 1.12);
см § 1.12);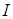 - интенсивность землетрясения;
- интенсивность землетрясения; - сейсмостойкость сооружения.
- сейсмостойкость сооружения. отвечает первой степени поражения сооружения, то есть повреждениям;
отвечает первой степени поражения сооружения, то есть повреждениям;  - второй, третьей, четвертой и пятой степеням поражения, то есть слабому, среднему, сильному и полному разрушениям соответственно.
- второй, третьей, четвертой и пятой степеням поражения, то есть слабому, среднему, сильному и полному разрушениям соответственно.