 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Обернена пропорційність, її властивості та графік.
4. Розглядаючи прямо пропорційні величини, ми встановили, що вони задаються формулою у= kх. Сформулюємо означення обернено пропорційних величин. Означення: дві величини називаються обернено пропорційними, якщо із збільшенням (зменшенням) однієї величини у кілька разів інша величина зменшується (збільшується) у стільки ж разів. Означення: функцією оберненої пропорційності називається функція виду у=k/х, де k≠0 і kєR. Розглянемо властивості функції у=k/х. Оскільки для знаходження значення у за відомим значенням х необхідно виконати дію ділення, яка в множині дійсних чисел не існує лише для ділення на нуль, то областю визначення цієї функції буде множина дійсних чисел крім нуля. Отже, D(k/x)=(-∞;0)È(0;+∞). Для визначення проміжків монотонності функції виберемо два довільних значення аргументу х1 і х2 таких, що х1>х2. Тоді 1/ х1<1/х2. Якщо k>0, то k/х1>k/х2, тобто f(х1)<f(х2). Це означає, що при k>0 функція оберненої пропорційності спадає на всій області визначення. Якщо k<0, то із нерівності 1/х1<1/х2 випливає k/х1>k/х2, тобто f(х1)>f(х2). Це означає, що при k<0 функція оберненої пропорційності зростає на всій області визначення. Для того, щоб визначити парною чи непарною є ця функція, відповідно до означення непарних функцій маємо: f(-х)=k/(-x)= -k/x= -f(х), тобто справедлива рівність f(-х)= -f(х). Це означає, що функція у=k/х є непарною, а її графік повинен бути симетричним відносно початку координат. Із шкільного курсу математики відомо, що графіком функції у=k/х є гіпербола, яка розміщена у першій та третій координатних кутах, якщо k>0, і в другій та четвертій чверті, якщо k<0. Особливою точкою функції є точка з координатами (0;0). Якщо х прямує до нуля, залишаючись меншим за х, то при k>0 функція у=k/х прямує до -∞. Якщо ж х прямує до нуля, залишаючись більшим за нуль, то функція прямує до +∞. Якщо х прямує до нуля, залишаючись меншим за х, то при k<0 функція у=k/х прямує до +∞. Якщо ж х прямує до нуля, залишаючись більшим за нуль, то функція прямує до -∞. Оскільки для кожного значення аргументу х≠0 і хєR, можна знайти відповідне йому значення функції уєR, яке не дорівнює нулю, то множиною значень функції у=k/х є множина таких дійсних чисел, для яких хє(-∞;0)È(0;+∞), тобто Е(k/x)=(-∞;0)È(0;+∞).
5*. Квадратична функція, її властивості та графік. 5. Означення: функція виду y=ax2+bx+c, a,b,cєR, a≠0 називається квадратичною функцією. Областю визначення квадратичної функції є множина всіх дійсних чисел, бо для знаходження значення функції за заданим значенням аргументу необхідно виконати дії додавання і множення, які в множині дійсних чисел завжди виконуються. Функція не відноситься ні до парних, ні до непарних, бо y(-x)=a(-x)2+b(-x)+c=ax2-bx+c=-(-ax2+bx-c), тобто не виконується жодна з рівностей f(-х)=f(х) чи f(-х)= -f(х). Знайдемо проміжки монотонності функції, виділивши попередньо повний квадрат:
6*. Операції над функціями та графіками, перетворення графіків. 6*. У математиці досить часто доводиться розв’язувати питання про те, які ж операції можна виконувати над функціями, як при цьому зміниться область визначення D(f) функції, як побудувати графік нової функції. Для того, щоб знайти відповіді на поставлені запитання, розглянемо кілька нових понять. Означення: сумою функцій f і g називають функцію f+g, яка визначена на множині D(f+g)=D(f)ÇD(g) та для якої виконується умова, що для будь-якого хєD(f+g) справедлива рівність [f+g](x)=f(x)+g(x). Означення: добутком функцій f і g називають функцію f•g, яка визначена на множині D(f•g)=D(f)ÇD(g) та для якої виконується умова, що для будь-якого хєD(f•g) справедлива рівність f•g(x)=f(x)•g(x). Для того, щоб одержати функції f+g чи f•g, якщо вони задані аналітично, слід додати чи помножити праві частини функцій. Проілюструємо це на конкретному прикладі. Вправа:знайти суму та добуток даних функцій y1=x3+3, хє[0;3] і у2=3х+2, хє[0;6]. Розв’язання. Спочатку знайдемо області визначення суми та добутку функцій. За означенням суми та добутку функцій D(f+g)=[0;3] і D(f•g)=[0;3]. Отже, y1+y2=x3+3+3х+2= x3+3х+5, а y1•y2=(x3+3)(3х+2)=3x4+2x3+9х+6, де хє[0;3]. Цілком зрозуміло, що операцію утворення з двох даних функцій їх суми чи добутку слід називати відповідно додаванням чи множенням функцій. При знаходження суми чи добутку функцій кількість доданків чи множників може бути як завгодно великою, але скінченною. Для того, щоб побудувати графік функції, яка є сумою двох функцій, необхідно додати відповідні ординати, а при побудові графіка добутку двох функцій – відповідні ординати слід перемножити. Покажемо це на конкретному прикладі. Вправа: побудувати графік функцій: а) у=х+│х│; б) у=х•│х│. Розв’язання. У системі координат будуємо графіки двох функцій: у1=х і у2=│х│. Після цього слід відповідно до означення додати відповідні ординати. Щоб це було легше зробити, використаємо означення модуля. Отже, розглянемо два випадки: 1) х≥0; 2) х<0. У першому випадку у1+у2=х+х=2х. Це означає, що на проміжку [0;+∞) графіком суми функцій буде пряма у=2х. Якщо х<0, то у1+у2=х+(-х)=х-х=0. Це означає, що на проміжку (-∞;0) графіком суми функцій буде пряма у=0. Як відомо, це вісь абсцис. Таким чином, графік функції у=х+│х│ складається з двох променів із спільним початком в точці з координатами О(0;0). Міркуючи аналогічно, можна прийти до висновку, що графік функції у=х•│х│ також складатиметься з двох частин: при х≥0 маємо у1•у2=х•х=х²; при х<0 будемо мати у1•у2=х•(-х)= -х². Таким чином, при х≥0 графіком функції у=х•│х│ буде вітка параболи у=х², а при х<0 – вітка параболи у=-х². Пропонуємо студентам виконати відповідні побудови самостійно. Цілком зрозуміло, що будувати графіки саме таким способом не завжди зручно. Саме тому в математиці сформульовані та доведені твердження, які надають можливість значно спростити відшукання відповіді на запитання: що ж будує графіком функції? Наприклад, як побудувати графік функції у=Af(ax+b)+B, де A, B, a, b – сталі, причому А≠0 і а≠0. Щоб дати відповідь на це запитання сформулюємо і приймемо без доведення наступні леми та наслідки з них. Лема 1: графік функції g(x), що визначається рівністю g(x)=f(x-α)+β, де (x-α)єD(f), а α і β – сталі, утворюється з графіка функції f паралельним перенесенням, при якому початок координат О(0;0) переходить в точку О′(α;β). Звернемо увагу на те, що при практичному використанні леми 1 діють інакше: через точку О′(α;β) проводять допоміжні осі координат О′х′ і О′у′. У системі координат х′О′у′ будують графік у′=f(х′). Цей графік відносно системи координат хОу і є графіком функції g(x)=f(x-α)+β. Лема 2: графік функції Із лем 1 і 2 випливають наступні наслідки. Наслідок 1: графік функції g, що визначається рівністю Наслідок 2: графік функції g, що визначається рівністю Наслідок 3: графік функції g, що визначається рівністю Користуючись лемами 1 і 2 та наслідками, розглянемо алгоритм побудови графіка функції 1) перетворити задану функцію до вигляду лем 1 і 2, тобто до виду у=Аf(a(x-α))+B; 2) у системі координат хОу через точку 3) у системі координат Вправа 1: побудувати графік функції Розв’язання. 1) перетворимо задану функцію до вигляду 2) з’ясуємо чому дорівнюють 3) оскільки 4) у системі координат хОу через точку О′(-5;2) проводимо допоміжні осі координат О′х′ і О′у′; 5) у системі координат х′О′у′ будуємо спочатку графік функції 6) у системі координат х′О′у′ будуємо графік функції 7) у системі координат х′О′у′ будуємо графік функції 8) побудована лінія відносно системи координат хОу є шуканим графіком. Цей графік є також гіперболою. Вправа 2: побудувати графік функції Розв’язання. 1) перетворимо задану функцію до вигляду
2) з’ясуємо чому дорівнюють 3) оскільки 4) у системі координат хОу через точку О′( 5) у системі координат х′О′у′ будуємо спочатку графік функції у=x²; 6) у системі координат х′О′у′ будуємо графік функції у′=-x′², як результат симетрії графіка функції у′=x′² відносно осі абсцис; 7) у системі координат х′О′у′ будуємо графік функції у′=-2x′², як результат розтягу графіка функції у′=-x′² відносно осі ординат; 8) побудована лінія відносно системи координат хОу є шуканим графіком. Цей графік є також параболою.
Запитання для самоконтролю та самостійної роботи студентів. 1. Довести по аналогії з властивістю 6, властивості 7 і 8 числових нерівностей. 2. Довести тотожність (а-b)²=а²-2аb+b². 3. Довести тотожність а²-b²=(а-b)(а+b). 4. Довести тотожність (а-b)³=а³-3а²b+3аb²-b³. 5. Довести тотожність а³+b³=(а+b)(а²-аb+b²). 6. Довести теорему 2 про рівносильність рівнянь. 7. Знайти множину допустимих значень змінної та множину розв’язків кожного із рівнянь: а) 8. Довести теореми про рівносильність рівнянь з двома змінними. 9. Знайти центр і радіус кола, заданого рівнянням 10. Записати рівняння кола, яке проходить через точки 11. Центр кола знаходиться в точці 12. Довести теорему 2 про рівносильність нерівностей. 13. Побудувати, заштрихувавши відповідну частину координатної площини, множини розв’язків нерівностей: х<а, х≤а, у>а, у≥а, у<а, у≤а, y≤kx+b,y³kx+b, (х-а)²+(у-b)²<R², (х-а)²+(у-b)²>R², (х-а)²+(у-b)²≤R², (х-а)²+(у-b)²≥R². 14. Дослідити функцію y=x2-5x+6 та побудувати графік. 15. Побудувати графік функцій: а) у=х+│х│; б) у=х•│х│.
Поиск по сайту: |
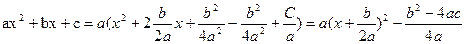 . Якщо a>0, то функція спадає на проміжку
. Якщо a>0, то функція спадає на проміжку 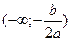 , а зростає на
, а зростає на  . Якщо a<0, то функція зростає на проміжку
. Якщо a<0, то функція зростає на проміжку  , при
, при 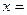
 . При a<0 функція має найбільше значення при
. При a<0 функція має найбільше значення при 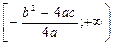 , а при a<0 -
, а при a<0 - 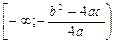 .
.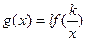 , де
, де  , а
, а 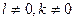 - сталі, утворюється з графіка функції f розтягом від осі абсцис з коефіцієнтом
- сталі, утворюється з графіка функції f розтягом від осі абсцис з коефіцієнтом 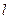 і наступним розтягом від осі ординат з коефіцієнтом k.
і наступним розтягом від осі ординат з коефіцієнтом k.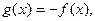 де
де 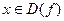 , утворюється з графіка функції f перетворенням симетрії відносно осі абсцис.
, утворюється з графіка функції f перетворенням симетрії відносно осі абсцис.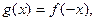 дн
дн  , утворюється з графіка функції f перетворенням симетрії відносно осі ординат.
, утворюється з графіка функції f перетворенням симетрії відносно осі ординат. де
де 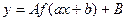 , якщо відомо графік функції
, якщо відомо графік функції 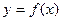 . Для цього перетворимо функцію: у виразі ах+b винесемо за дужки число а, тоді отримаємо
. Для цього перетворимо функцію: у виразі ах+b винесемо за дужки число а, тоді отримаємо 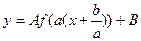 . Позначимо
. Позначимо 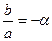 , а тоді у=Аf(a(x-α))+B. Отже, щоб побудувати графік функції
, а тоді у=Аf(a(x-α))+B. Отже, щоб побудувати графік функції  проводимо допоміжні осі координат
проводимо допоміжні осі координат  і
і 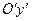 ;
; будуємо графік функції
будуємо графік функції 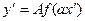 як результат розтягу графіка функції
як результат розтягу графіка функції  від осі абсцис з коефіцієнтом А і наступного розтягу від осі ординат з коефіцієнтом
від осі абсцис з коефіцієнтом А і наступного розтягу від осі ординат з коефіцієнтом 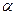 . Побудований графік є шуканим. Проілюструємо сказане на наступних прикладах.
. Побудований графік є шуканим. Проілюструємо сказане на наступних прикладах.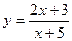 .
.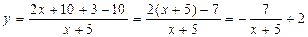 ;
; . Оскільки
. Оскільки  , то графік функції
, то графік функції  слід будувати, перетворюючи графік
слід будувати, перетворюючи графік  . Графіком цієї функції є гіпербола;
. Графіком цієї функції є гіпербола; де
де 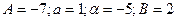 , то будуємо систему координат хОу;
, то будуємо систему координат хОу; ;
;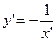 як результат симетрії графіка функції
як результат симетрії графіка функції 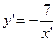 як результат розтягу графіка функції
як результат розтягу графіка функції 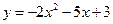 .
.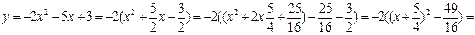
 ;
; , а=1, b=
, а=1, b= 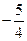 , то графік функції
, то графік функції 
 , де А=-2, В=
, де А=-2, В=  ; б)
; б) 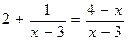 .
. .
.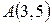 та
та  , і має радіус 12.
, і має радіус 12. і має радіус 7. Записати його рівняння.
і має радіус 7. Записати його рівняння.