Системи та сукупності нерівностей з однією змінною та способи їх розв’язування. Нерівності та системи нерівностей з двома змінними, графічний спосіб їх розв’язування.

3. Розглядаючи рівняння та нерівності з однією та двома змінними, системи та сукупності рівнянь з двома змінними, ми давали відповідні означення. Аналогічно можна визначити поняття системи та сукупностей нерівностей, та інші поняття які пов’язані з ними.

Означення: системою двох нерівностей з однією змінною, заданих на одній і тій самій множині, називається кон’юнкція цих нерівностей.

Означення: сукупністю двох нерівностей з однією змінною, заданих на одній і тій самій множині, називається диз’юнкція цих нерівностей.

Символічно систему двох нерівностей з однією змінною в загальному вигляді позначають так: f₁(х)<g₁(х)Ùf₂(х)<g₂(х) або

f₁(х)<g₁(х)

f₂(х)<g₂(х). Відповідно сукупність двох нерівностей з однією змінною в загальному вигляді позначають так: f₁(х)<g₁(х)Úf₂(х)<g₂(х) або

f₁(х)<g₁(х)

f₂(х)<g₂(х).

Означення: розв’язати систему нерівностей - це означає знайти такі значення змінної із множини хєХ, які перетворюють кожну нерівність системи в істинну числову нерівність.

Означення: розв’язати сукупність нерівностей - це означає знайти такі значення змінних хєХ, які задовольняють хоча б одну нерівність сукупності.

Вище ми визначили поняття системи і сукупності нерівностей з однією і двома змінними, з’ясували, що означає розв’язати систему або сукупність нерівностей, а тепер перейдемо до розгляду способів їх розв’язання. Найбільш поширеними серед цих способів є наступні: а) графічний спосіб; б) аналітичний спосіб. Суть першого полягає в тому, що в одній й тій самій системі координат зображають множину розв’язків кожної нерівності системи чи сукупності. Потім для системи нерівностей шукають перетин множин розв’язків, тобто спільні розв’язки всіх нерівностей системи. Для знаходження множини розв’язків сукупності нерівностей шукають об’єднання множин розв’язків кожної нерівності сукупності, тобто ті розв’язки, які задовольняють хоча б одну нерівність сукупності. В математиці під графіком нерівності розуміють множину її розв’язків, зображених на координатній площині. У математиці доведені наступні твердження, які допомагають при графічному розв’язуванні систем і сукупностей нерівностей.

Твердження 1: множиною розв’язків нерівності х>а (х³а) є права півплощина, на які пряма х=а поділяє координатну площину (у випадку х³а разом з прямою х=а) (див. малюнок № 6.5.).

Малюнок № 6.5. Множина розв’язків нерівностей х>а і х³а .

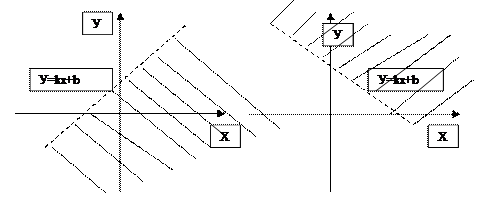
Твердження 2: множиною розв’язків нерівності х<а (х≤а) називається ліва півплощина, на які пряма х=а розбиває координатну площину (у випадку х≤а разом з прямою у=а).

Твердження 3: множиною розв’язків нерівності у>а (у≥а) є верхня із півплощин, на які пряма у=а розбиває координатну площину (у випадку у³а разом з прямою у=а).

Твердження 4: множиною розв’язків нерівності у<а (у≤а) є нижня півплощина, на які пряма у=а розбиває координатну площину (у випадку у≤а разом з прямою у=а).

Твердження 5: множиною розв’язків нерівності y<kx+b є нижня із півплощин, на які ця пряма розбиває координатну площину, без прямої y=kx+b.

Твердження 6: множиною розв’язків нерівності y>kx+b є верхня із півплощин, на які ця пряма розбиває координатну площину, без прямої y=kx+b (див. малюнок № 6.6.).

Твердження 7: множиною розв’язків нерівності y≤kx+b є нижня із півплощин, на які пряма у=kx+b розбиває координатну площину, разом з прямою у=kx+b.

Твердження 8: множиною розв’язків нерівності y³kx+b є верхня із півплощин, на які пряма у=kx+b розбиває координатну площину, разом з прямою у=kx+b.

Твердження 9: множиною розв’язків нерівності (х-а)²+(у-b)²<R² є та частина координатної площини, яка знаходиться всередині кола з центром в точці (а,b) і радіусом R без точок кола (х-а)²+(у-b)²=R².

Малюнок № 6.6. Множина розв’язків нерівностей y<kx+b і y>kx+b.

Твердження 10: множиною розв’язків нерівності (х-а)²+(у-b)²>R² є та частина координатної площини, яка знаходиться поза колом з центром в точці (а,b) і радіусом R без точок кола (х-а)²+(у-b)²=R².

Твердження 11: множиною розв’язків нерівності (х-а)²+(у-b)²≤R² є та частина координатної площини, яка знаходиться всередині кола з центром в точці (а,b) і радіусом R з точками кола (х-а)²+(у-b)²=R².

Твердження 12: множиною розв’язків нерівності (х-а)²+(у-b)²≥R² є та частина координатної площини, яка знаходиться поза колом з центром в точці (а,b) і радіусом R з точками кола (х-а)²+(у-b)²=R² .

Із розв’язанням систем і сукупностей нерівностей, досить часто доводиться зустрічатися при розв’язанні дробово-раціональних нерівностей та нерівностей, одна частина яких є добутком, а інша дорівнює 0. Покажемо це на конкретному прикладі.

Вправа: розв’язати нерівність: , обґрунтовуючи виконувані дії теоремами про рівносильність нерівностей.

Розв’язання.

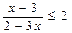Знайдемо область визначення нерівності. 2-3х≠0↔3х≠2↔х≠2/3. Із нерівності на основі теорем про рівносильність нерівностей маємо: 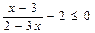↔ ↔ . Звідси отримуємо таку сукупність систем нерівностей:

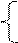7х-7≥0 7х≥7 х≥1 х≥1

2-3х<0 3х>2 х>2/3

7х-7≤0 7х≤7 х≤1

2-3х>0 3х<2 х<2/3 х<2/3.

Таким чином, множиною розв’язків заданої нерівності буде множина: (-∞;2/3)È[1;+∞).

Поиск по сайту: