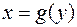|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Геометричний зміст визначеного інтеграла
Якщо функція
Якщо Тоді за формулою (4.1) маємо
  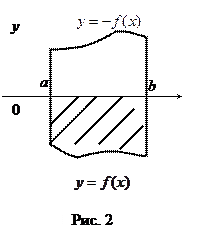
Формули (4.1) і (4.2) можна об’єднати в одну:
Якщо функція

Приклад 4.1.Знайти площі фігур, обмежених даними лініями: а) параболою б) параболою Розв’язання а) Виконаємо (рис. 4).

Застосуємо формулу (4.1). Одержимо
б) Виконаємо рисунок (рис. 5).

Функція
Якщо плоска фігура обмежена двома неперервними кривими

Приклад 4.2. Знайти площу фігури, обмеженої даними лініями:
Розв’язання. Для того, щоб обчислити площу заданої фігури, необхідно: а) побудувати плоску фігуру, обмежену заданими лініями; б) визначити межі інтегрування; в) обчислити відповідний визначений інтеграл.

Виконаємо рисунок (рис. 7). Рівняння верхньої лінії
За формулою (4.5):
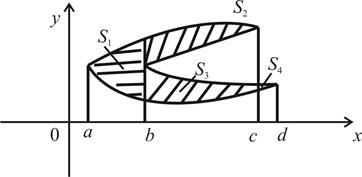
Якщо плоска фігура має складнішу форму (рис. 8), то прямими, паралельними оси ОY, її треба розбити на скінчену суму фігур, площі яких знаходяться за формулою (4.5). Тоді площа S дорівнюватиме сумі знайдених площ фігур (на рис. 8
Рис. 8
Приклад 4.3. Знайти площу фігури, обмеженої даними лініями:
Розв’язання
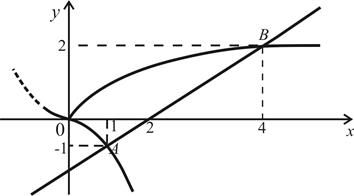
Рис. 9
Виконаємо рисунок (рис. 9). Знайдемо абсциси точок перетину ліній, що обмежують фігуру. Лінії Щоб знайти абсцису точки перетину ліній
Отже абсциса точки перетину цих ліній x=4. Абсциса точки перетину ліній
Запишемо рівняння верхньої ліній що обмежують фігуру:
Оскільки нижня лінія задається при різних значеннях х різними аналітичними виразами, розіб’ємо фігуру на дві частини прямою
Якщо криволінійна трапеція обмежена лініями

Приклад 4.4. Знайти площу фігури, обмеженої лініями
Розв’язання. Виконаємо рисунок (рис. 11).
 
Поиск по сайту: |
 є неперервною на відрізку
є неперервною на відрізку  то визначений інтеграл
то визначений інтеграл  являє собою площу криволінійної трапеції – фігури, обмеженої лініями
являє собою площу криволінійної трапеції – фігури, обмеженої лініями  (рис 1):
(рис 1):




 , то фігура, обмежена лініями
, то фігура, обмежена лініями 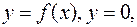
 (рис. 2) не є криволінійною трапецією. Площа цієї фігури дорівнює
(рис. 2) не є криволінійною трапецією. Площа цієї фігури дорівнює  .
.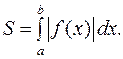 (4.3)
(4.3) скінченне число разів змінює знак (рис. 3), то за формулою (4.3) маємо:
скінченне число разів змінює знак (рис. 3), то за формулою (4.3) маємо: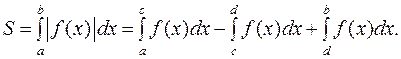 (4.4)
(4.4)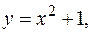 прямими
прямими 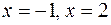 і віссю абсцис
і віссю абсцис  ;
; прямою
прямою  і осями координат
і осями координат 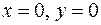 .
.


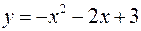
 на відрізку
на відрізку 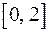 змінює знак, а саме:
змінює знак, а саме:  Для знаходження шуканої площі S скористаємося формулою (4.4):
Для знаходження шуканої площі S скористаємося формулою (4.4):
 і
і 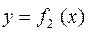
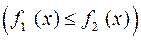 и двома вертикальними прямими
и двома вертикальними прямими  (рис. 4), то її площа обчислюється за формулою (4.5):
(рис. 4), то її площа обчислюється за формулою (4.5): . (4.5)
. (4.5)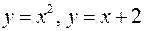 .
.
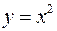
 Рис. 7
Рис. 7 нижньої лінії
нижньої лінії 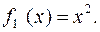 Визначимо межі інтегрування. Для цього обчислимо абсциси точок перетину прямої
Визначимо межі інтегрування. Для цього обчислимо абсциси точок перетину прямої  .
. .
.
 ).
).

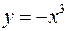


 , розв’яжемо рівняння
, розв’яжемо рівняння

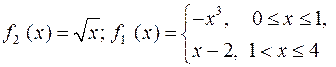
 . Застосовуючи формулу (4.5), одержимо:
. Застосовуючи формулу (4.5), одержимо: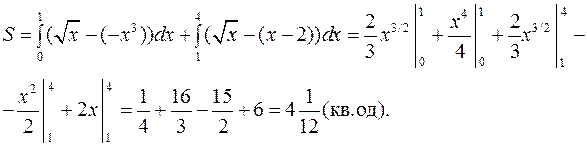
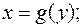
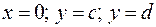 (рис. 10) то формула для обчислення її площі має вигляд (4.6):
(рис. 10) то формула для обчислення її площі має вигляд (4.6):