 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Естественный (или натуральный) способ задания движения
Этот способ используют, когда известна траектория АВ движения точки (рис. 6). Траекторией в данном случае будет геометрическое место последовательных положений движущейся точки по отношению к данной системе отсчета. На траектории АВ выберем неподвижную точку О, которую примем за начало отчета. С течением времени точка будет занимать положения М, М1, М2, …, определяемые координатами S, S1, S2, и т.д. Следовательно, чтобы знать положение точки на траектории в любой момент времени, надо знать зависимость: Таким образом, чтобы задать движение естественным способом необходимо задать: 1) траекторию точки; 2) начало О и направление отсчета положительных и отрицательных дуговых координат S, определяющих положение точки М на траектории (рис. 6); 3) закон движения точки по траектории
При естественном способе задания движение точки рассматривают в естественных осях (осях естественного трехгранника). Естественные оси координат (скоростные оси, оси естественного трехгранника) Проведем в точке М кривой АВ соприкасающуюся плоскость, нормальную плоскость, перпендикулярную касательной, и спрямляющую плоскость, перпендикулярную соприкасающейся и нормальной плоскостям, образующую с этими плоскостями естественный трехгранник (рис. 7).
Рис. 7. Оси естественного трехгранника
Естественными координатными осями называются три взаимно перпендикулярные оси: касательная, направленная в сторону возрастания дуговой координаты, главная нормаль, направленная в сторону вогнутости кривой, и бинормаль, направленная по отношению к касательной и главной нормали также, как ось Oz направлена по отношению к осям Ox и Oy в правой системе координатных осей. Единичные векторы-орты этих осей обозначаются соответственно Естественные оси попарно образуют координатные плоскости (грани естественного трехгранника): ( ( ( Естественные оси имеют начало в точке M кривой и при движении точки M по этой кривой перемещаются вместе с ней, оставаясь взаимно перпендикулярными, но изменяя свое направление в пространстве. Определение скорости точки при естественном способе задания движения Пусть дана траектория АВ точки М и задан закон движения точки по траектории
Пусть в момент времени t точка занимает положение M, а в момент времени t1=t + Δt – положение M1. Дуговые координаты этих точек имеют следующие значения: Проведем из произвольного центра
Введем в качестве промежуточной переменной дуговую координату S, от которой, очевидно, зависит радиус-вектор Тогда скорость точки М равна:
где
Следовательно:
Значит,
Алгебраическая величина скорости точки Скорость точки определяется производной по времени t от дуговой координаты. Вектор скорости точки направлен по касательной к траектории в сторону движения (в сторону возрастания дуговой координаты), если
Вектор кривизны траектории Возьмем на траектории две точки М и М1 (рис. 9, а) с координатами Покажем орты касательных Определим приращение вектора
Разделим приращение орта
Направление этого вектора совпадает с направлением вектора приращения орта касательной Предел, к которому стремиться вектор средней кривизны кривой, когда
Вектор кривизны кривой в данной точке равен производной от орта касательной к кривой по дуговой координате. Определим модуль и направление вектора
Модуль Из дифференциальной геометрии известно, что предел отношения угла Таким образом:
Угол
При Следовательно,
Окончательно, вектор кривизны кривой равен произведению орта Определение ускорения точки при задании ее движения естественным способом Вектор скорости точки определяется из выражения Вектор ускорения точки равен:
или Ускорение точки равно геометрической сумме двух векторов, один из которых направлен по главной нормали и называется нормальным ускорением точки, а другой направлен по касательной и называется касательным ускорением точки.
Модуль касательного ускорения точки равен
где знак «плюс», полученный в ответе после вычисления дроби, соответствует ускоренному движению точки, а знак «минус» – замедленному. Модуль нормального ускорения точки определяется по формуле:
Бинормальное ускорение точки всегда равно нулю, т.к. точка всегда находится в соприкасающейся плоскости:
Поиск по сайту: |
 - закон движения точки по траектории.
- закон движения точки по траектории. (как функцию дуговой координаты от времени).
(как функцию дуговой координаты от времени).

 ,
,  и
и  .
. ,
, 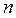 ) – соприкасающаяся плоскость,
) – соприкасающаяся плоскость, ) – спрямляющая плоскость,
) – спрямляющая плоскость,
 и
и 
 , где
, где  – приращение дуговой координаты.
– приращение дуговой координаты. в точку М радиус-вектор, тогда скорость этой точки будет равна:
в точку М радиус-вектор, тогда скорость этой точки будет равна: .
. движущейся точки. Таким образом, радиус-вектор является сложной функцией времени:
движущейся точки. Таким образом, радиус-вектор является сложной функцией времени: 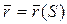 , т.к.
, т.к.  .
. ,
,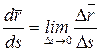 , при
, при  вектор
вектор  (направлен также как и вектор
(направлен также как и вектор  ) стремится к направлению касательной в соответствующей точке в сторону увеличения дуговой координаты. Модуль этого вектора стремится к единице:
) стремится к направлению касательной в соответствующей точке в сторону увеличения дуговой координаты. Модуль этого вектора стремится к единице: .
.
 – есть орт касательной. Тогда скорость точки М равна:
– есть орт касательной. Тогда скорость точки М равна: .
. .
. , или в обратную сторону, если
, или в обратную сторону, если  .
. и
и  .
. и
и  в точках М и М1. Модули орт постоянны
в точках М и М1. Модули орт постоянны  при перемещении точки по кривой. Следовательно, орт
при перемещении точки по кривой. Следовательно, орт  =
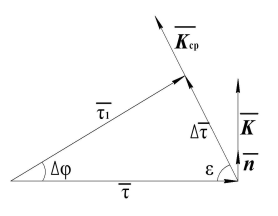
=  . Для этого построим в точке М векторный параллелограмм со сторонами
. Для этого построим в точке М векторный параллелограмм со сторонами  и диагональю
и диагональю  .
.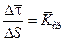 – вектор, характеризующий поворот касательной к кривой на некотором участке ММ1, называется вектором средней кривизны кривой на этом участке ММ1 (рис. 9, б).
– вектор, характеризующий поворот касательной к кривой на некотором участке ММ1, называется вектором средней кривизны кривой на этом участке ММ1 (рис. 9, б). , называется вектором кривизны кривой в данной точке:
, называется вектором кривизны кривой в данной точке: .
. (рис. 9, б).
(рис. 9, б). а) Построение векторного параллелограмма
а) Построение векторного параллелограмма
 б) Построение вектора
б) Построение вектора 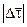 найдем как длину основания равнобедренного треугольника с малым углом
найдем как длину основания равнобедренного треугольника с малым углом  при вершине и боковыми сторонами, равными единице. Тогда:
при вершине и боковыми сторонами, равными единице. Тогда:  .
. , где
, где  – радиус кривизны кривой в данной точке.
– радиус кривизны кривой в данной точке. .
. при основании равнобедренного треугольника равен:
при основании равнобедренного треугольника равен: .
.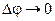 ,
, 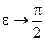 .
. перпендикулярен орту
перпендикулярен орту  ,
, .
. .
. ,
, .
. – касательное ускорение точки, существующее лишь при неравномерном движении точки и характеризующее изменение модуля скорости точки.
– касательное ускорение точки, существующее лишь при неравномерном движении точки и характеризующее изменение модуля скорости точки.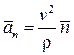 – нормальное ускорение точки, существующее лишь при криволинейном движении точки и характеризующее изменение направления скорости точки.
– нормальное ускорение точки, существующее лишь при криволинейном движении точки и характеризующее изменение направления скорости точки. , т.к.
, т.к.  и
и  , то:
, то: , или
, или ,
, ,
, .
.