 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Линейное программирование с параметром в целевой функции
Пусть коэффициент cj целевой функции изменяется в пределах (cj — c'j,cj + с''j), тогда для удобства решения задачи его можно заменить выражением
где c'j, с''j — постоянные; λ — параметр, который изменяется в некоторых пределах (в общем случае от - В общем виде задача линейного программирования с параметром в целевой функции записывается так:
при ограничениях:
Для каждого значения λ в промежутке δ ≤ λ ≤ φ, где δ и φ — произвольные действительные числа, найти вектор Решая задачу на максимум симплексным методом и исследуя ее решение в зависимости от изменения параметра λ, получим выражения для определения нижнего (λ1) и верхнего (λ2) его значений:
где Δ"j, — оценка симплексной таблицы, содержащая параметр λ; Δ'j — оценка симплексной таблицы, не содержащая параметр λ. Если для целевой функции отыскивается min, то границы изменения λ (λ1 и λ2) определяются следующим образом:
Приведем алгоритм решения. 1) Задачу решаем симплекс-методом при конкретном значении параметра λ до получения оптимального решения. 2) Вычисляем значения параметров λ1, λ2. 3) Определяем множество значений параметра λ, для которых полученное решение является оптимальным. 4) В случае необходимости в базис вводим вектор, соответствующий столбцу, из которого определялось значение параметра λ2. 5) Выбираем ключевую строку и ключевой элемент. 6) Определяем новое оптимальное решение. 7) Находим новое множество значений λ, для которых решение останется оптимальным. 8) Процесс вычисления повторяем до тех пор, пока весь отрезок [δ, φ] не будет исследован. Выясним геометрический смысл задачи.
Пусть L(
Поиск по сайту: |
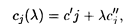
 до
до 

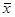 (x1, x2,..., xп), удовлетворяющий системе ограничений и обращающий в максимум (минимум) целевую функцию.
(x1, x2,..., xп), удовлетворяющий системе ограничений и обращающий в максимум (минимум) целевую функцию.


 (c'j + λc''jxj) → max. ABCDEF — область допустимых решений (рис. 25.1). При λ = 0 строим вектор
(c'j + λc''jxj) → max. ABCDEF — область допустимых решений (рис. 25.1). При λ = 0 строим вектор  и, перемещая линию уровня MN по направлению вектора
и, перемещая линию уровня MN по направлению вектора  (D)опт и L(
(D)опт и L(