 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Алгоритм сложения в коде 8-4-2-1
1. Проверить знаки слагаемых – отрицательные преобразовать в обратный код, инвертируя тетрады и прибавляя потетрадно код 1010. Единицы переноса между тетрадами отбрасывать. 2. Сложить двоично-десятичные числа по правилам двоичной арифметики. 3. Выполнить коррекцию результата, прибавив код 0110 к «неправильным» тетрадам, а также к тетрадам, из которых сформировались единицы переноса. Единицы переноса между тетрадами учитывать. 4. Проверить знак результата – отрицательный перевести в прямой код, инвертируя тетрады и прибавляя потетрадно код 1010. Единицы переноса между тетрадами отбрасывать. Пример.Сложить десятичные числа А=-85,1 и В=39,9 в коде 8-4-2-1. Масштабируем операнды М=102 и кодируем цифры чисел в ПК. Апк = 1,1000.0101.0001. Впк = 0,0011.1001.1001. Отрицательное число А переводим в ОК: инверсия 1,0111.1010.1110. Единицы переноса коррекция 1010.1010.1010. отбрасывать! Аок 1,0001.0100.1000. Выполняем сложение чисел в ОК: Аок =1,0001.0100.1000. Вок = 0,0011.1001.1001. 1,0100.1110.0001. коррекция .0110.0110. (А+В)ОК =1,0101.0100.0111. Сумма отрицательная – переводим в ПК: инверсия 1,1010.1011.1000.Единицы переноса коррекция .1010.1010.1010. отбрасывать! (А+В)ПК= 1,0100.0101.0010. Умножение на масштаб и перевод в десятичную систему счисления позволяет убедиться в правильности полученного результата: (А+В)=-0100.0101,0010 = -45,2.
2. Код с избытком три 8-4-2-1+3
Это модификация кода с естественными весами, обеспечивающая выполнение свойства самодополняемости. Прямые коды десятичных цифр получают прибавлением тройки к двоичным эквивалентам цифр. Обратные коды получают простым инвертированием тетрад прямого кода. Действительно: 15–(Ак+3) = =12-Ак= (9-Ак)+3. Однако обретение свойства самодополняемости привело к утрате свойства однозначности веса каждого разряда. При сложении в коде 8-4-2-1+3 могут возникнуть следующие два случая, требующие введения коррекции. Таблица 3.
1. Sk Sk=(Ak+3)+(Bk+3)+Ck =(Ak+Bk+Ck)+6. Сформировался избыток 6, а нужен избыток 3, следовательно, необходима коррекция кодом: -310 = - 00112 = 1101ДК 2. Sk Sk = (Ak +3)+(Bk +3)+Ck-16=(Ak+Bk+Ck)-10. Естественно формируется перенос из данной тетрады, а избытка 3 нет, следовательно, нужна коррекция кодом: +3=00112.
Алгоритм сложения в коде 8-4-2-1+3
1. Проверить знаки слагаемых – отрицательные перевести в ОК путём инвертирования тетрад. 2. Сложить двоично-десятичные числа по правилам двоичной арифметики. 3. Выполнить коррекцию результата: - прибавить код 0011 к тетрадам суммы, из которых формировались единицы переноса; - прибавить код 1101 к тетрадам суммы, из которых не формировались единицы переноса. При коррекции единицы переноса между тетрадами отбрасывать. 4. Проверить знак результата – отрицательный перевести в ПК путём инвертирования тетрад. Таким образом, код стал самодополняемым, однако, все тетрады надо корректировать, что требует дополнительного времени. Пример.Сложить десятичные числа А =-85,7 и В =-39,4 в коде 8-4-2-1+3. Чтобы избежать ПРС при сложении чисел одинакового знака, выбираем масштаб операндов с «запасом» - М=103 и кодируем цифры чисел в ПК: АПК=1,0011.1011.1000.1010. ВПК=1,0011.0110.1100.0111. Переводим отрицательные числа в ОК и складываем: АОК=1,1100.0100.0111.0101. ВОК=1,1100.1001.0011.1000. 11,1000.1101.1010.1101. Возникла единица переноса из знакового разряда, которую следует прибавить к младшей тетраде. Кроме того, для выполнения коррекции необходимо зафиксировать наличие или отсутствие переносов между тетрадами (указаны в виде верхних индексов в скобках): 1,(1)1000.(0)1101.(0)1010.(0)1110. 0011. 1101. 1101. 1101. коррекция (А+В)ОК= 1, 1011. 1010. 0111. 1011. единицы переноса отбрасывать! Переводим результат в ПК путём инвертирования тетрад: (А+В)ПК=1,0100.0101.1000.0100.=-125,110
Код Айкена 2-4-2-1 Таблица 4.
Этот код можно рассматривать как код с естественными весами для первых пяти цифр 0,1,2,3,4,а для остальных пяти цифр это код с избытком 6. Код имеет свойство самодополняемости (сумма весов двоичных разрядов равна 9), так что обратный код любой тетрады можно получить инвертированием. Единственный недостаток этого кода в том, что старший разряд двоичной тетрады имеет искусственный вес. Из особенностей формирования десятичных цифр вытекают следующие правила введения коррекции при алгебраическом сложении. Предварительно рассмотрим возможные варианты формирования тетрад суммы. 1. Обе исходные тетрады меньше 5, и единица переноса из данной тетрады не формируется. Здесь возможны два случая: а) тетрада суммы тоже меньше 5, результат будет получен верный, значит, коррекция не нужна; б) тетрада суммы больше или равна 5, значит, для таких цифр надо искусственно сформировать избыток 6, следовательно, нужна коррекция кодом +610=01102. 2. Одна исходная тетрада меньше 5, а другая больше или равна 5. В этом случае возможны два варианта: а) если нет переноса из тетрады суммы: SK= AK+(BK+6)+CK – результат верный, коррекции нет. б) если есть перенос из тетрады суммы в соседнюю старшую тетраду: SK= AK+(BK+6)+CK-16= AK+BK+CK-10 - результат верный, коррекции нет.
3. Обе исходных тетрады больше или равны 5,значит, есть единица переноса из тетрады суммы в соседнюю старшую тетраду: SK=(AK+6)+(BK+6)+CK-16=(АК+ВК+СК-10)+6 Здесь возможны два следующих варианта: а) если тетрада суммы больше или равна 5 – результат верный, коррекции нет; б) если тетрада суммы меньше 5, не нужен избыток 6, значит, необходима коррекция кодом -610=-01102=1010ДК. Таким образом, при алгебраическом сложении в коде 2-4-2-1 коррекция необходима в двух случаях: 1)если тетрады слагаемых меньше 5, тетрада суммы больше 4, необходима коррекция кодом плюс 6=0110; 2)если тетрады слагаемых больше или равны 5, есть единица переноса из тетрады суммы, а сама тетрада суммы меньше 5, нужна коррекция кодом минус 6=1010.
Поиск по сайту: |
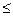9 – нет переноса из данной тетрады:
10 – есть перенос из данной тетрады: