 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Алгоритм деления с восстановлением остатков
В основе алгоритма деления лежит логика ручного счета. При выполнении деления на бумаге вычислитель быстро анализирует, что больше – делитель или делимое (очередной остаток), и когда делимое меньше делителя, в очередной разряд частного заносится «0» и выполняется сдвиг. В ЦВМ такой анализ можно сделать посредством вычитания делителя из делимого, и при получении отрицательного остатка в очередной разряд частного занести «0», а отрицательный остаток восстановить до предшествующего значения, прибавив к нему делитель. Только после этого можно выполнить сдвиги. Если же остаток положителен, в частное заносится «1» и выполняются соответствующие способу деления сдвиги. Это позволяет сформулировать алгоритм деления с восстановлением остатков для дробных чисел с фиксированной запятой (ФЗ): 1. Определить знак частного сложением по модулю 2 знаковых разрядов делимого и делителя. Далее использовать модули операндов. 2. Вычесть из делимого делитель путем сложения в обратном или дополнительном кодах. 3. Проанализировать знак остатка после первого вычитания: - если остаток положительный, произошло ПРС, операцию прекратить до смены масштабов операндов; - если остаток отрицательный, в частное занести «0» (этот разряд по окончании деления станет знаковым разрядом частного) и восстановить остаток, прибавив к нему делитель. 4. Выполнить сдвиги: частного на один разряд влево и остатка на один разряд влево (I способ) или делителя на один разряд вправо (II способ). 5. В цикле формирования цифр частного: вычесть из остатка делитель, прибавив его в обратном или дополнительном кодах. 6. Проанализировать знак полученного остатка: - если остаток положителен, в частное занести «1»; - если остаток отрицателен, в частное занести «0». 7. Восстановить отрицательный остаток, сложив его с делителем. 8. Выполнить сдвиги, как указано в пункте 4 алгоритма. 9. Завершить цикл формированием (n+1)–го остатка для округления. Последний сдвиг частного не выполнять. 10. Выполнить округление результата и присвоить частному знак, полученный в пункте 1 алгоритма. В соответствии с вышеизложенным алгоритмом можно представить формулой правила формирования очередного остатка для I и II способов деления. Пусть D – делитель, Di – остаток на i-м шаге алгоритма. В I способе деления выполняется сдвиг влево на один разряд (удвоение) остатка (восстановленного - (Di+D) или невосстановленного Di):
Во II способе деления выполняется сдвиг вправо на один разряд делителя, то есть уменьшение делителя вдвое:
Анализ приведенного алгоритма позволяет отметить следующие недостатки: -процесс деления ацикличен, так как операция восстановления остатка появляется нерегулярно, что приводит к усложнению устройства управления делением; -быстродействие алгоритма невелико, так как примерно в половине шагов цикла выполняется дополнительная операция восстановления остатка.
Пример 8. Разделитьчисла А=27(10) и В=-30(10), представив числа в форме с ФЗ в ПК (МА,В=25). Пусть А=0,11011 –делимое; В=1,11110-делитель. 1. Знак частного: 0Å1=1. 2. Деление модулей операндов выполним I способом с использованием ДК при вычитании.
1. Так как седьмой остаток положительный, то в отбрасываемый разряд частного должна быть занесена «1», следовательно, для округления результата к младшему разряду частного нужно прибавить единицу Тогда модуль частного после округления: А/В=0,11101. 2. Частное со знаком в прямом коде:(А/В)ПК= 1,11101. Проверка: А/В= -0,11101(2)=-0,90625(10).. Точный результат –(27/30)=-0,9. Пример 9. Разделить А=-25(10) на В=9(10), представив операнды в форме с ФЗ в прямом коде (МА,В=25). А=1,11001 – делимое; В=0,01001 – делитель. 1. Знак частного: 1Å0=1. 2. Деление модулей операндов выполним II способом с использованием ДК при вычитании.
3. Округленное частное в прямом коде: А/В=1,10110
Проверка: М=МА/МВ=27/25=22. А/В= -10,110(2)=-2,75(10). Точный результат –(25/9)=-2,78; относительная погрешность =1,08%.
Поиск по сайту: |
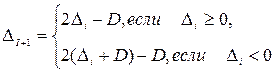 (1)
(1) (2)
(2)

 0,00000
0,00000

 0,00011
0,00011
 0,00111
0,00111
 0,01110
0,01110
 0,11100
0,11100


 0,00000
0,00000
 0,00001
0,00001
 0,00010
0,00010
 0,00101
0,00101
 0,01011
0,01011
 0,10110
0,10110
 0,10110(0)
0,10110(0)